Circumferences
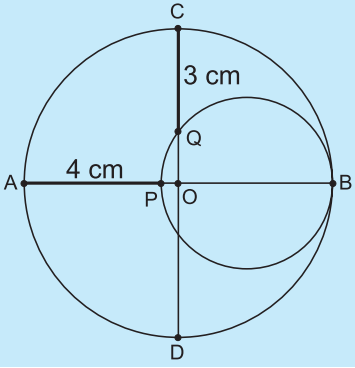 In the image above these two circumferences are tangent at point B. Find the radius of the smaller circle.
In the image above these two circumferences are tangent at point B. Find the radius of the smaller circle.
The answer is 2.5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
OP, How do you know that MP=R-4
Log in to reply
First note that ( M P ) is the radius of the smaller circle and that ( M P ) = R − 2 , and not R − 4 . To see why, since the diameter of the larger circle is 2 R , the diameter of the smaller circle will be
2 R − ( A P ) = 2 R − 4 = 2 ∗ ( R − 2 ) .
The radius of the smaller circle will then be half of this, i.e., R − 2 .
how do you know that (OP) = R-4?
Log in to reply
From the diagram we have that (AO) = (AP) + (OP), and so (OP) = (AO) - (AP). Now (AO) = R and (AP) = 4, so (OP) = R - 4.
We can apply Power of a Point Theorem here. Let the radius of the larger circle be x . We have ( x − 3 ) 2 = x ( x − 4 ) . Solving this yields x = 2 9 . We know that A B is a diameter of ∘ O , so it has length 2 ⋅ 2 9 = 9 . We also know that P B is a diameter of the smaller circle. We have P B = A B − A P = 9 − 4 = 5 , so the diameter of the smaller circle is 5 , and the diameter is 2 5 = 2 . 5
Hehe, you mean radius not diameter.
denote h=OP ( 4 + h ) h = ( 1 + h ) 2 2 h = 1 h = 2 1 r = 2 5 = 2 . 5
Do you mean O Q 2 = O P ⋅ O A ? How do you know this?
Log in to reply
This is a regular expression in right three-angles
Let R be the radius of the larger circle, and let M be the center of the smaller circle. Then
( M Q ) 2 = ( O Q ) 2 + ( M O ) 2 .
Now ( O Q ) = R − 3 ,
( M Q ) = ( M P ) = 2 1 ( 2 R − 4 ) = R − 2 , and
( M O ) = ( M P ) − ( O P ) = ( R − 2 ) − ( R − 4 ) = 2 .
So we have that
( R − 2 ) 2 = ( R − 3 ) 2 + 2 2 ⟹ R 2 − 4 R + 4 = R 2 − 6 R + 9 + 4
⟹ 2 R = 9 ⟹ R = 4 . 5 .
So the radius of the smaller circle is ( M Q ) = R − 2 = 2 . 5 .