Circumradius Party!
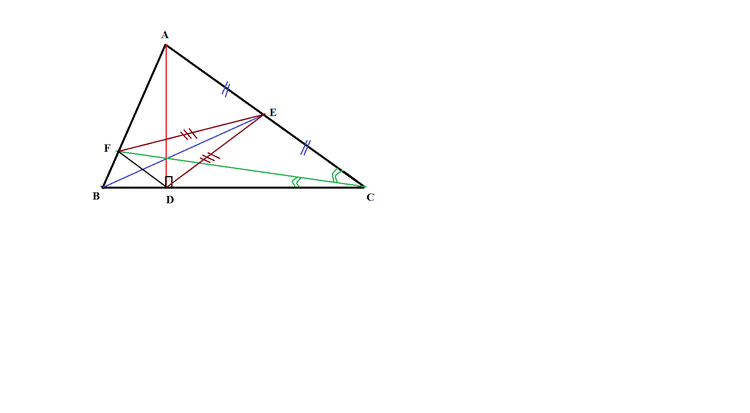 In
,
is the perpendicular from
onto
,
is the median and
is the internal angle bisector of
such that
is on
,
on
and
on
. Suppose that
,
and
are concurrent. If
unis, find
In
,
is the perpendicular from
onto
,
is the median and
is the internal angle bisector of
such that
is on
,
on
and
on
. Suppose that
,
and
are concurrent. If
unis, find
Details and assumptions : length of the circumradius of
The answer is 2.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
0 solutions
No explanations have been posted yet. Check back later!