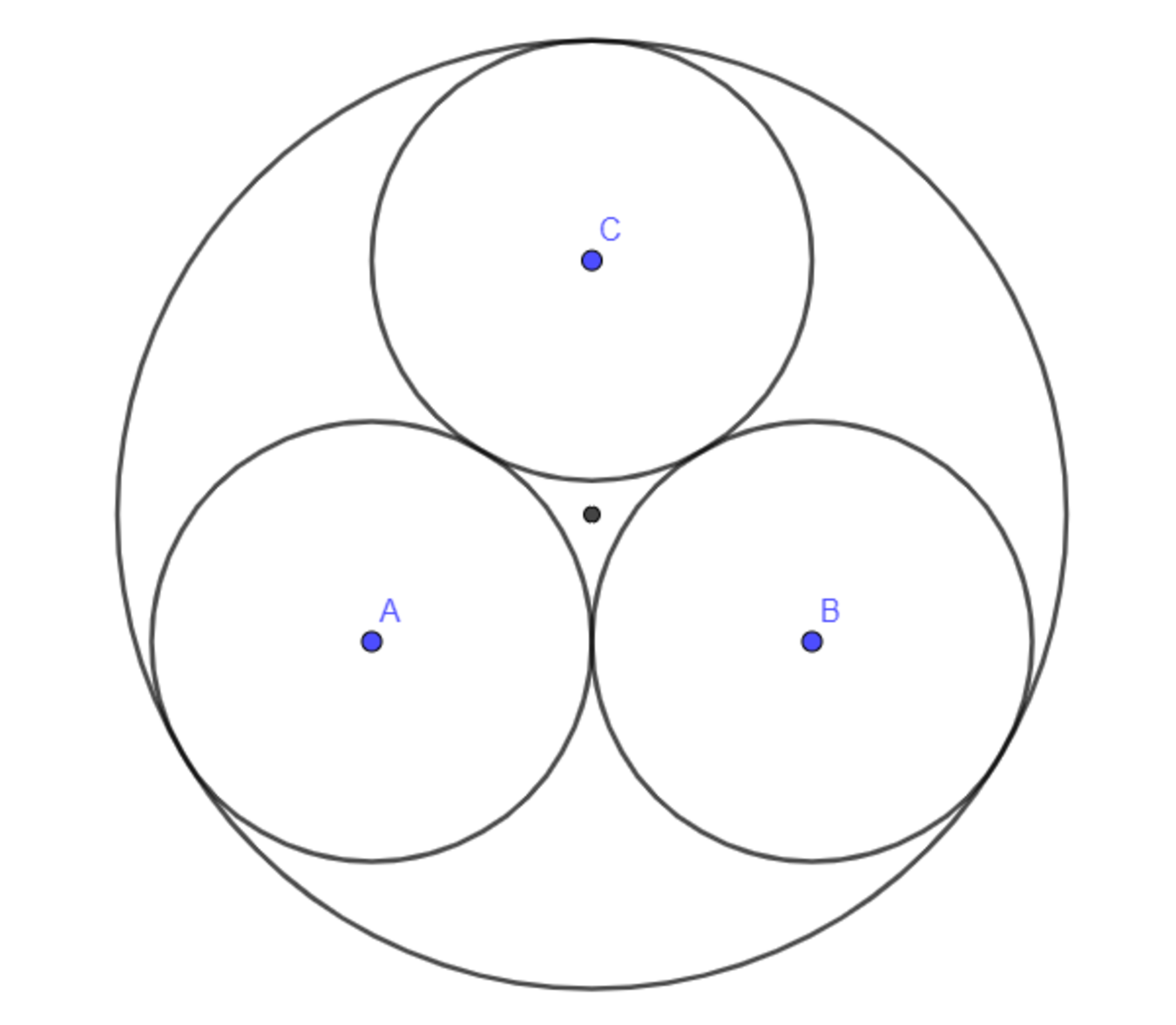
Circumscribed Circle

As shown above, in $\triangle OAF$ , $\cos \angle OAF=\frac{AF}{OA}$ $\implies \cos 30^{\circ}=\frac{5}{OA} \;\;\;$ $\;\;\;\;\;\;\;\implies OA=\frac{5}{\cos 30^{\circ}}=\frac{10}{\sqrt{3}}$ The radius of the larger circle is, $\begin{aligned} R &=OG \\ &=OA+AG \\ &=\frac{10}{\sqrt{3}}+5 \end{aligned}$ Therefore, $R=\dfrac{10}{\sqrt{3}}+5\implies a+b+c=\boxed{18}$

---

Alternative: Applying the Kissing Circle Theorem , $k_1=k_2=k_3=-\frac{1}{5}$ $\begin{aligned} \implies k_4 &=k_1+k_2+k_3+2\sqrt{k_1k_2+k_2k_3+k_3k_1} \\ &=-\frac{3}{5}+\frac{2\sqrt{3}}{5} \end{aligned}$ $\;\;\;\;\;\implies R=\frac{1}{k_4}=\frac{5}{2\sqrt{3}-3}=\frac{10\sqrt{3}+15}{3}=\frac{10\sqrt{3}}{3}+5$

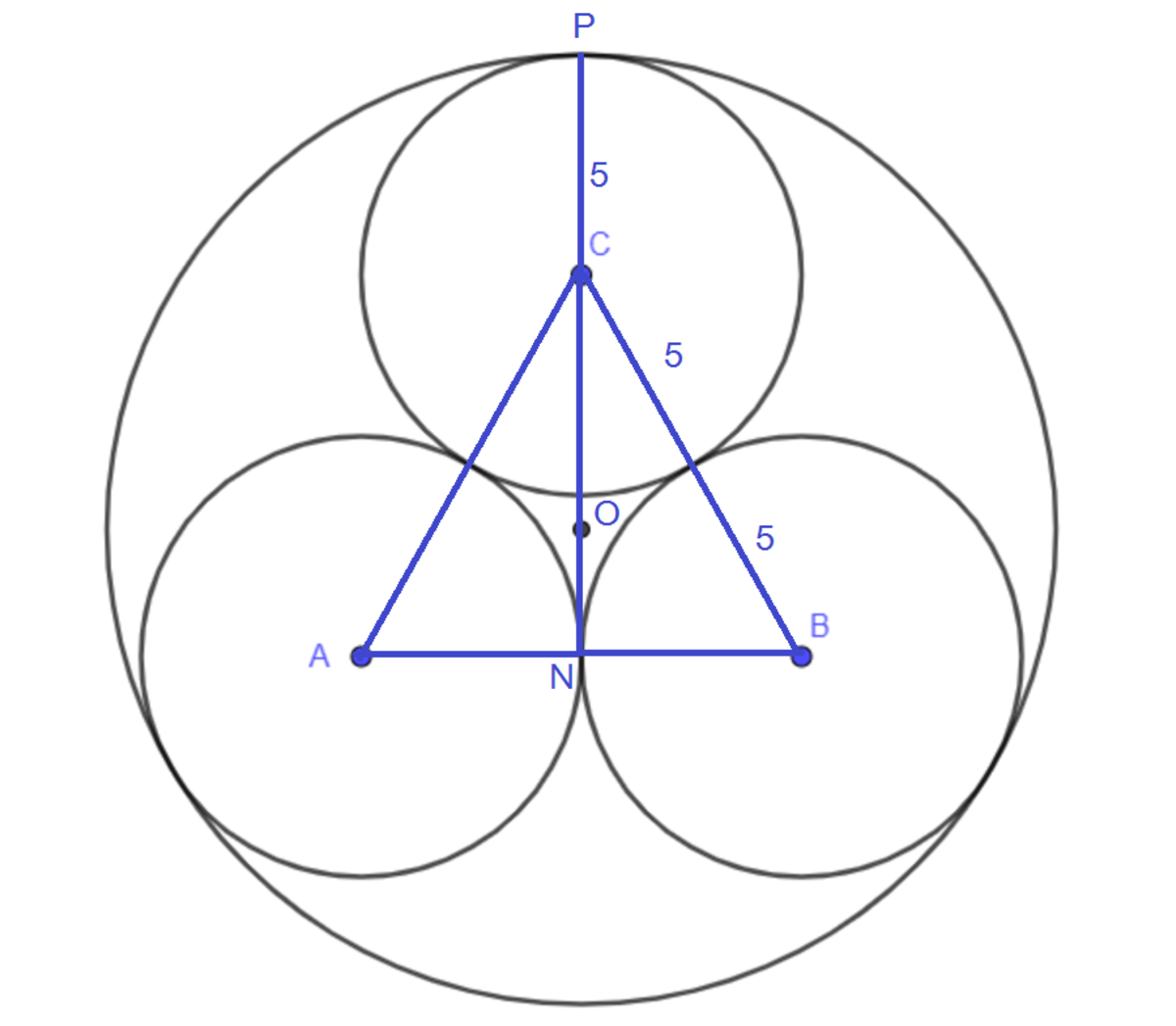
Joint the centers of the three congruent circles with line segments and we get an equilateral $\triangle ABC$ with side length $10$ . Let the center of the large circle be $O$ . We note that $O$ is also the centroid of $\triangle ABC$ . Let $ON$ be a median of $\triangle ABC$ . Then $ON = \dfrac {\sqrt 3}2 \times 10 = 5\sqrt 3$ . For a triangle the distance between centroid and vertex is twice the distance between the centroid to the base. Then $OC = \dfrac 23 ON = \dfrac 23 \times 5 \sqrt 3 = \dfrac {10}{\sqrt 3}$ . Since the radius of the big circle $R = OP = OC+CP = \dfrac {10}{\sqrt 3} + 5$ . Therefore $a+b+c = 10+3+5 = \boxed{18}$ .