Circumscribed quadrilateral

Geometry Level 4

Quadrilateral $ABCD$ is circumscribed about a circle $I$ , that is tangent to $AB, BC, CD, DA$ at $E, F, G, H,$ respectively. Suppose that $AC$ and $BD$ intersect at point $P$ and $EG$ and $FH$ intersect at point $Q$ . If $AB=5, BC=6, CD=8, DA=7$ , what is the distance between $P$ and $Q?$

The answer is 0.

2 solutions

Vin Bia
Aug 19, 2017

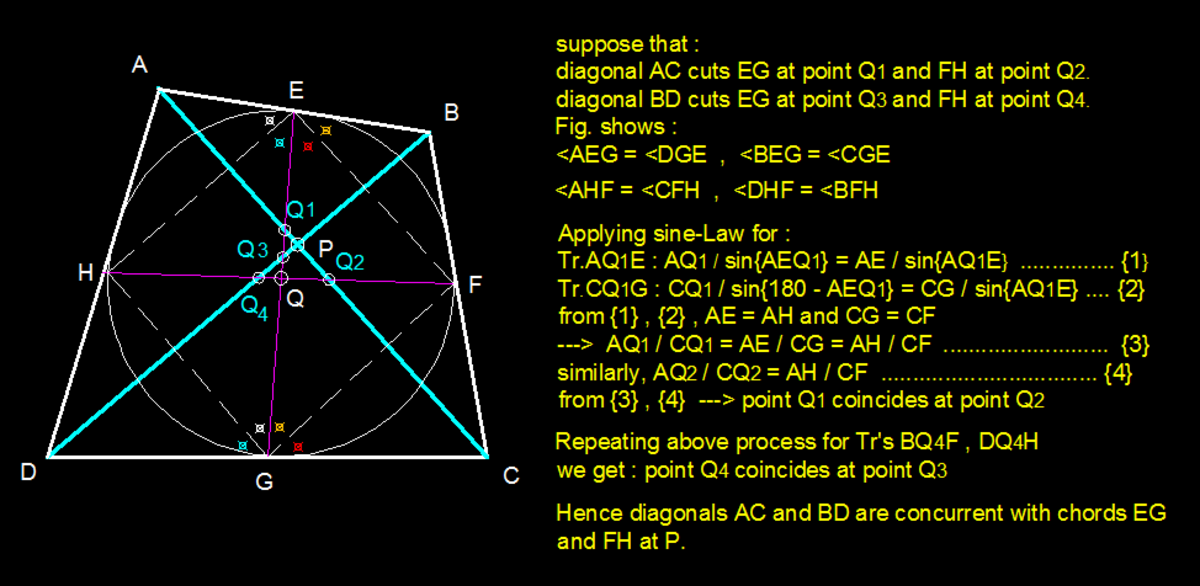
First, "hexagon" AEBCGD is circumscribed about I, since all 6 of its sides are tangent. Thus, by Brianchon's Theorem, AC, EG, and BD all concur. Since AC and BD intersect at P, we have that EG passes through P. Similarly, by Brianchon's Theorem on ABFCDH, we have that FH passes through P as well. Therefore, EG and FH intersect at P, so P and Q are the same point.

Ahmad Saad
Mar 17, 2016

how are ang(AHF) and ang(CFH) equal?

Ayush Pattnayak - 3 years, 2 months ago

Circumscribed quadrilateral

The answer is 0.

2 solutions

0 pending reports