Circumscribed Stacked Squares
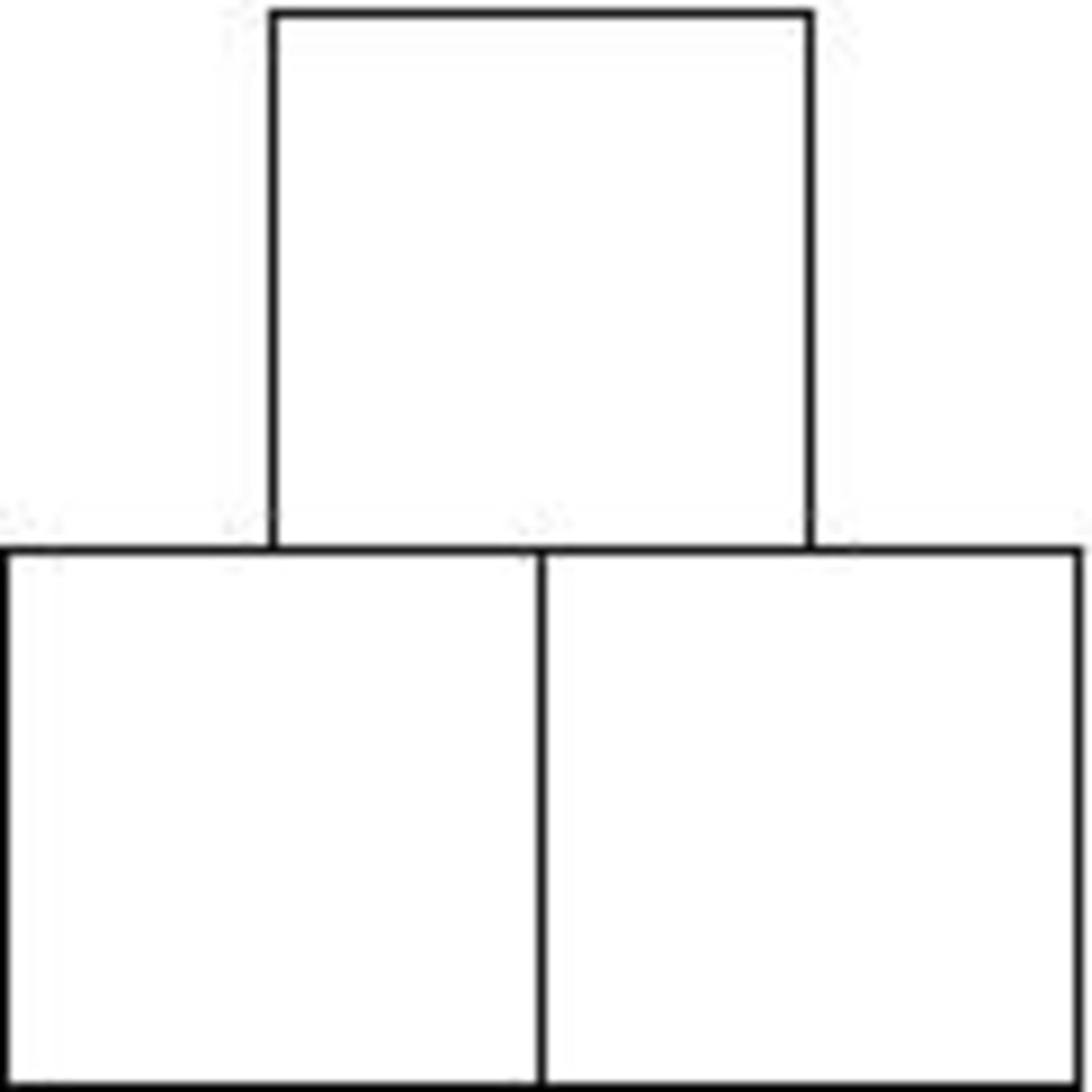
Three squares, all with side lengths , are placed so that two share a common side and the third is centered on top of the bottom two as in the figure below. The radius of the smallest circle containing all three squares is . Determine .
The answer is 425.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The circle of smallest radius will pass through the top two vertices of the square on top, and also the bottom rightmost vertex and the bottom leftmost vertex of the bottom squares. This circle's center will be on the common side of the two bottom squares. Let x denote the distance from the center of the circle to the bottom vertex of the common side of the two bottom squares. Then 1 6 − x is the distance from the center of the circle to the top vertex of the common side of the two bottom squares, and 3 2 − x is the distance from the center to the top of the top square. Let r denote the radius of the circle.
By the Pythagorean Theorem, r 2 = 8 2 + ( 3 2 − x ) 2 , and also r 2 = 1 6 2 + x 2 . Therefore, 8 2 + ( 3 2 − x ) 2 = 1 6 2 + x 2 , and when we simplify this equation the x 2 terms cancel and we get 8 3 2 = 6 4 x . Therefore x = 1 3 and r 2 = 1 6 2 + 1 3 2 = 4 2 5 .