Circumscribed Triangle - Three tangent circles
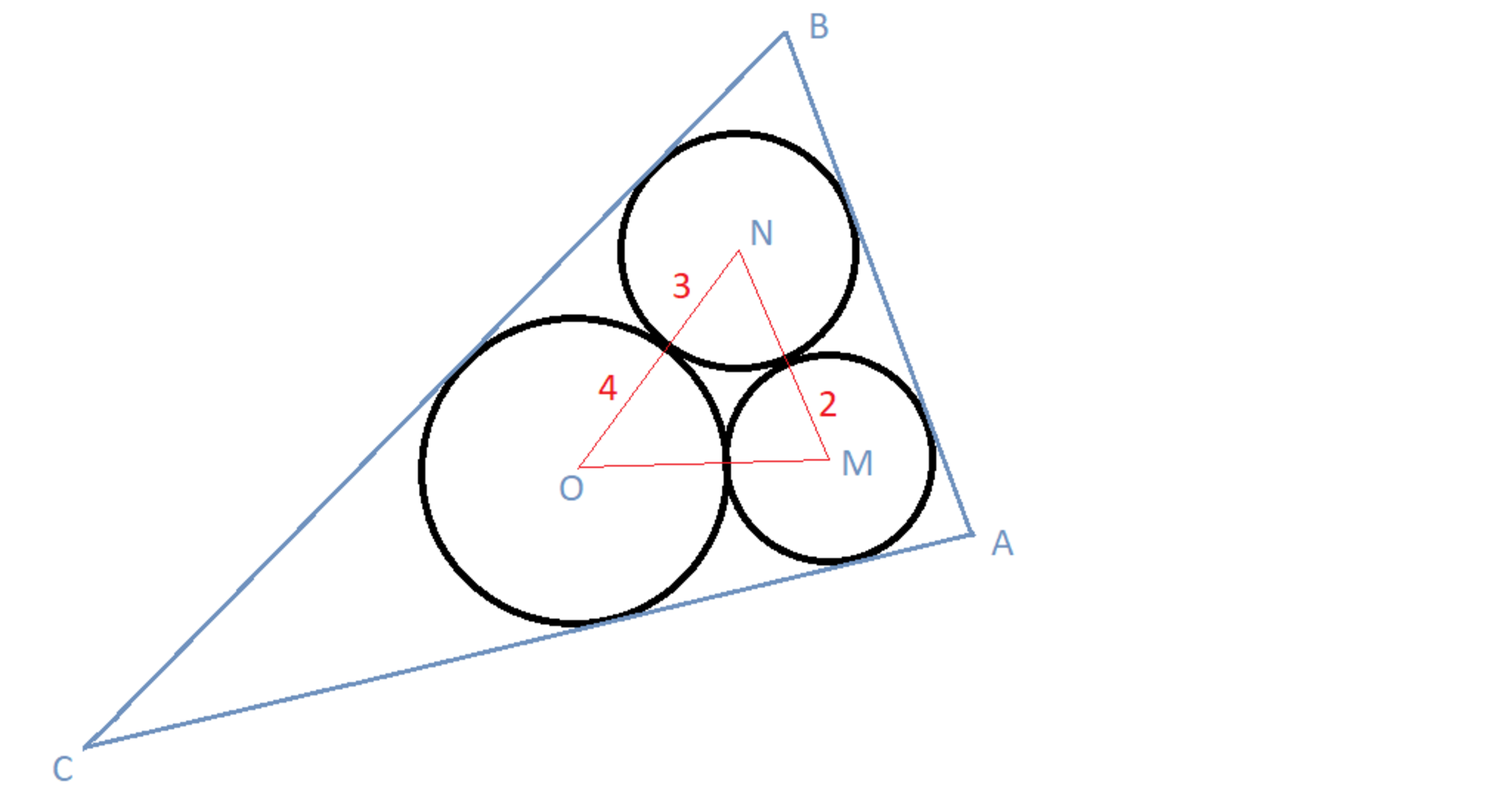
Circles have radii of . They are positioned such that each one is tangent to the other two. is drawn tangent to the circles and surrounding them as shown in the figure above. Find the area of .
Figure not drawn to scale
The answer is 197.538.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Assume O to be the origin (0,0). Then M:(6,0) and N may be determined as (5,2√6). The three circles are: x²+y²=36, (x-6)²+y²=4, (x-5)²+(y-2√6)²=9. The direct tangents can be determined as: y-0.35x+4.24=0, y-0.73x-4.96=0 and x=8. Solving these equations two at a time gives us the vertices of the outer triangle which are: [-24.2105,-12.7137], [8,-1.44] & [8,10.8]. The area of the triangle formed by these three vertices may be calculated by the shoe-lace formula viz. 2A =x1(y2-y3)+x2(y3-y1)+x3(y1-y2). A=197.128