Circumscribing a hexagonal prism
A right hexagonal prism with a regular hexagonal base of side length a = 1 0 , and height h = 3 0 , is to be inscribed in a regular tetrahedron of edge length A , such that three alternating edges of the hexagonal top base of the prism are in contact with the three (non-horizontal) faces of the tetrahedron. Find A .
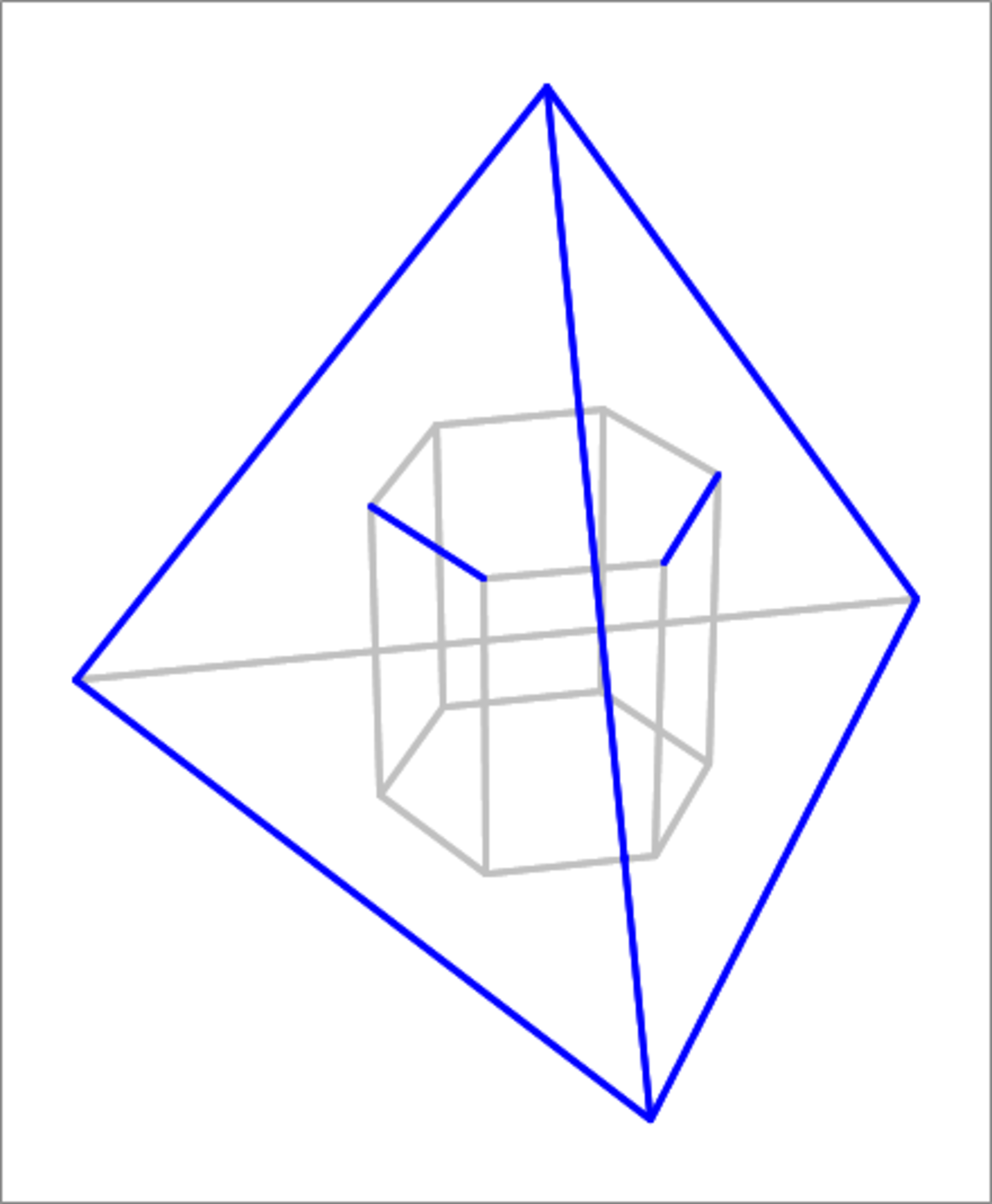
The answer is 66.74.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Extending the lines of the Hexagon will create a triangle of side length
3
a
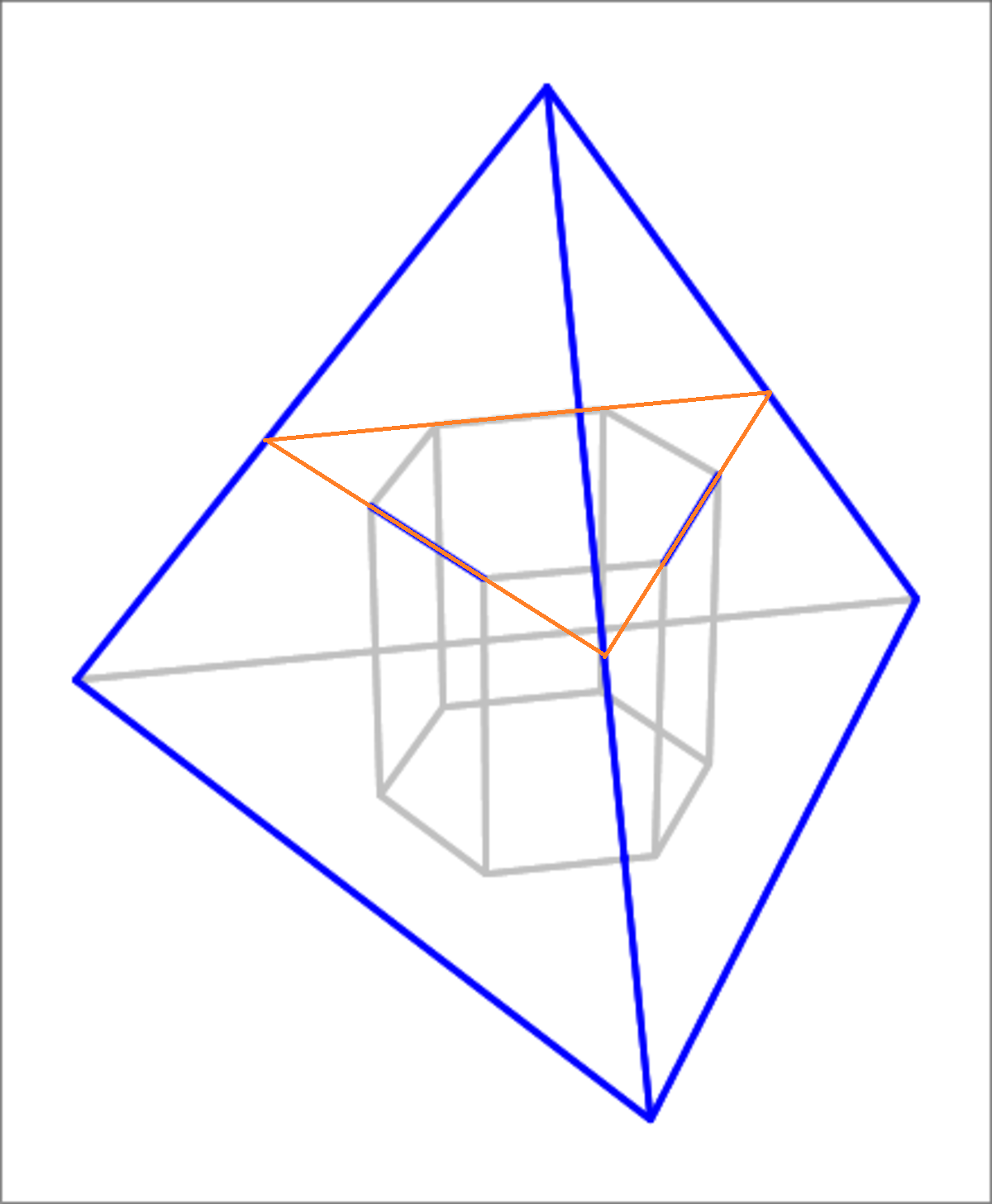
Fomula for Tetrahedron's heigt: H = 3 A 6
Wich makes A = 6 3 H
The total height is the prism's height + the smaller tetrahedron's height (on top of the prism)
H = h + 3 3 a 6
A = 6 3 ( h + 3 3 a 6 ) = 6 3 h + 3 9 a 6 ) = 6 6 . 7 4
Label the diagram as follows:
Since B C = 2 1 A and ∠ C B O = 3 0 ° , B O = 3 3 A and C O = 6 3 A .
Since B H = A and B O = 3 3 A , by the Pythagorean Theorem on △ B H O , H O = 3 6 A .
Since △ G E C ∼ △ H O C by AA similarity, E G C E = H O C O . Substituting E G = 3 0 , C O = 6 3 A , and H O = 3 6 A and solving gives C E = 2 1 5 2 .
E O is the height of equilateral △ D F O with a side length of D F = 1 0 , so E O = 5 3 .
By segment addition, C O = C E + E O . Substituting C O = 6 3 A , C E = 2 1 5 2 , and E O = 5 3 and solving gives A = 1 5 6 + 3 0 ≈ 6 6 . 7 4 .