CircumTriangle

Geometry Level 5

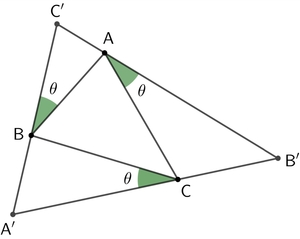A △ A ′ B ′ C ′ \triangle A'B'C' circumscribes another △ A B C \triangle ABC such that ∠ A B C ′ = ∠ B C A ′ = ∠ C A B ′ {\angle ABC'=\angle BCA'=\angle CAB'} as shown in the figure.

Find the maximum ratio of the area of △ A ′ B ′ C ′ \triangle A'B'C' to the area of △ A B C \triangle ABC in terms of the angles A A , B B and C C .

Submit your answer for A = π 7 , B = 2 π 7 A=\frac{\pi}{7}, B=\frac{2\pi}{7} and C = 4 π 7 C=\frac{4\pi}{7} .


The answer is 8.

Digvijay Singh by Digvijay Singh , 21, India

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

2 solutions

Mark Hennings
Jan 15, 2021

I shall relabel the points somewhat, since it makes what follows easier to read (and write!). Angle chasing shows that ∠ A A 1 B = A \angle AA_1B = A , ∠ B B 1 C = B \angle BB_1C = B and ∠ C C 1 A = C \angle CC_1A = C , where A , B , C A,B,C are the angles of triangle A B C ABC . Thus A B C ABC and A 1 B 1 C 1 A_1B_1C_1 are similar, and so the area ratio r = ∣ A 1 B 1 C 1 ∣ ∣ A B C ∣ = ( A 1 B 1 A B ) 2 = ( c 1 c ) 2 r \; =\; \frac{|A_1B_1C_1|}{|ABC|} \; =\; \left(\frac{A_1B_1}{AB}\right)^2 \; = \; \left(\frac{c_1}{c}\right)^2 in an obvious extension of standard notation. Now c 1 = A 1 B + B B 1 = c sin ⁡ ( A + θ ) sin ⁡ A + a sin ⁡ θ sin ⁡ B = c ( sin ⁡ ( A + θ ) sin ⁡ A + sin ⁡ A sin ⁡ θ sin ⁡ B sin ⁡ C ) \begin{aligned} c_1& =\; A_1B + BB_1 \; = \; c\frac{\sin(A+\theta)}{\sin A} + a\frac{\sin\theta}{\sin B} \\ & = \; c\left(\frac{\sin(A+\theta)}{\sin A} + \frac{\sin A \sin \theta}{\sin B \sin C}\right) \end{aligned}

and hence c 1 c = cos ⁡ θ + ( cot ⁡ A + sin ⁡ A sin ⁡ B sin ⁡ C ) sin ⁡ θ \frac{c_1}{c} \; = \; \cos\theta + \left(\cot A + \frac{\sin A}{\sin B \sin C}\right)\sin\theta which means that the maximum area ratio is r m a x = 1 + ( cot ⁡ A + sin ⁡ A sin ⁡ B sin ⁡ C ) 2 = 1 + ( b 2 + c 2 − a 2 4 Δ + a 2 2 Δ ) 2 = 1 + ( a 2 + b 2 + c 2 4 Δ ) 2 = 1 + ( 4 R 2 ( sin ⁡ 2 A + sin ⁡ 2 B + sin ⁡ 2 C ) 4 × 2 R 2 sin ⁡ A sin ⁡ B sin ⁡ C ) 2 = 1 + ( sin ⁡ 2 A + sin ⁡ 2 B + sin ⁡ 2 C ) 2 4 sin ⁡ 2 A sin ⁡ 2 B sin ⁡ 2 C \begin{aligned} r_{\mathrm{max}} & = \; 1 + \left(\cot A + \frac{\sin A}{\sin B \sin C}\right)^2 \; = \; 1 + \left(\frac{b^2 + c^2 - a^2}{4\Delta} + \frac{a^2}{2\Delta}\right)^2 \\ & = \; 1 + \left(\frac{a^2 + b^2 + c^2}{4\Delta}\right)^2 \; = \; 1 + \left(\frac{4R^2(\sin^2A + \sin^2B +\sin^2C)}{4 \times 2R^2 \sin A \sin B \sin C}\right)^2 \\ & = \; 1 + \frac{(\sin^2A + \sin^2B + \sin^2C)^2}{4\sin^2A\sin^2B\sin^2C} \end{aligned} where Δ \Delta is the area of the triangle A B C ABC and R R is the circumradius of A B C ABC .

In this case, cos ⁡ 2 1 7 π \cos^2\tfrac17\pi , cos ⁡ 2 2 7 π \cos^2\tfrac27\pi , cos ⁡ 2 4 7 π \cos^2\tfrac47\pi are the roots of the equation F ( X ) = 64 X 3 − 80 X 2 + 24 X − 1 F(X) \; = \; 64X^3 - 80X^2 + 24X - 1 and hence we deduce that, sin ⁡ 2 A + sin ⁡ 2 B + sin ⁡ 2 C = 3 − ( cos ⁡ 2 A + cos ⁡ 2 B + cos ⁡ 2 C ) = 3 − 80 64 = 7 4 4 sin ⁡ 2 A sin ⁡ 2 B sin ⁡ 2 C = 4 ( 1 − cos ⁡ 2 A ) ( 1 − cos ⁡ 2 B ) ( 1 − cos ⁡ 2 C ) = 1 16 F ( 1 ) = 7 16 \begin{aligned} \sin^2A + \sin^2B + \sin^2C & = \; 3 - (\cos^2A + \cos^2B + \cos^2C) \; = \; 3 - \tfrac{80}{64} \; = \; \tfrac74 \\ 4\sin^2A\sin^2B\sin^2C & = \; 4(1 - \cos^2A)(1-\cos^2B)(1-\cos^2C) \; = \; \tfrac{1}{16}F(1) \; = \; \tfrac{7}{16} \end{aligned} and hence r m a x = 1 + ( 7 4 ) 2 7 16 = 1 + 7 = 8 r_{\mathrm{max}} \; = \; 1 + \frac{\big(\frac{7}{4}\big)^2}{\frac{7}{16}} \; = \; 1 + 7 = \boxed{8}

2 Helpful 1 Interesting 7 Brilliant 0 Confused

r max r_\text{max} is also equal to csc ⁡ 2 ω \csc^2{\omega} , where ω \omega is the Brocard angle of △ A B C \triangle ABC .

r max = csc ⁡ 2 ω = csc ⁡ 2 A + csc ⁡ 2 B + csc ⁡ 2 C r_\text{max}=\csc^2{\omega}=\csc^2{A}+\csc^2{B}+\csc^2{C}

Digvijay Singh - 4 months, 4 weeks ago

Log in to reply

Indeed, as I commented, seven months ago, here

Mark Hennings - 4 months, 4 weeks ago

@Mark Hennings can you explain how you came up with F ( x ) F(x) and how it is related to these cosines?

Veselin Dimov - 4 months, 3 weeks ago

Log in to reply

This is standard fare using complex numbers. If we suppose that ξ 7 = 1 \xi^7=1 but ξ ≠ 1 \xi\neq1 , then since ( ξ − 1 ) ( ξ 6 + ξ 5 + ξ 4 + ξ 3 + ξ 2 + ξ + 1 ) = ξ 7 − 1 = 0 (\xi-1)(\xi^6 + \xi^5 + \xi^4 + \xi^3 + \xi^2 + \xi + 1) = \xi^7 - 1 = 0 we have 0 = ξ 3 + ξ 2 + ξ + 1 + ξ − 1 + ξ − 2 + ξ − 3 = ( ξ + ξ − 1 ) 3 + ( ξ + ξ − 1 ) 2 − 2 ( ξ + ξ − 1 ) − 1 = ζ 3 + ζ 2 − 2 ζ − 1 \begin{aligned} 0 & = \; \xi^3 + \xi^2 + \xi + 1 + \xi^{-1} + \xi^{-2} + \xi^{-3} \; = \; (\xi+\xi^{-1})^3 + (\xi + \xi^{-1})^2 - 2(\xi +\xi^{-1}) - 1 \\ & = \; \zeta^3 + \zeta^2 - 2\zeta - 1 \end{aligned} where ζ = ξ + ξ − 1 \zeta = \xi+\xi^{-1} . But this means that G ( X ) = X 3 + X 2 − 2 X − 1 G(X) \; = \; X^3 + X^2 - 2X - 1 has zeros 2 cos ⁡ 2 k π 7 2\cos\tfrac{2k\pi}{7} for 1 ≤ k ≤ 6 1 \le k \le 6 , and so, removing repeats, for k = 1 , 2 , 3 k = 1,2,3 . Thus F ( Y ) = G ( 4 Y − 2 ) = 64 Y 3 − 80 Y 2 − 24 Y − 1 F(Y) \; = \; G(4Y-2) \; = \; 64Y^3 - 80Y^2 - 24Y - 1 has zeros cos ⁡ 2 k π 7 \cos^2\tfrac{k\pi}{7} for k = 1 , 2 , 3 k=1,2,3 , and so the roots are cos ⁡ 2 1 7 π \cos^2\tfrac17\pi , cos ⁡ 2 2 7 π \cos^2\tfrac27\pi and cos ⁡ 2 4 7 π \cos^2\tfrac47\pi .

Mark Hennings - 4 months, 3 weeks ago

Log in to reply

Wow! That's cool! And is much faster and more reliable in general than my method I think! Sadly I didn't know this 2 years ago when we had to calculate such trig products and sums in school. I would've surprised my math teacher.

Veselin Dimov - 4 months, 3 weeks ago
Veselin Dimov
Jan 18, 2021

It's not hard to find that ∠ C ′ = ∠ A , ∠ A ′ = ∠ B , ∠ B ′ = ∠ C \angle C'=\angle A, \angle A'=\angle B, \angle B'=\angle C . This implies △ A B C ∼ △ C ′ A ′ B ′ \triangle ABC \sim \triangle C'A'B' . Let the ratio the problem is asking for be k ² = A A ′ B ′ C ′ A A B C k²=\frac{A_{A'B'C'}}{A_{ABC}} . Then we have: k = A A ′ B ′ C ′ A A B C = A ′ C ′ c k=\sqrt{\frac{A_{A'B'C'}}{A_{ABC}}}=\frac{A'C'}{c} I use a = B C ; b = A C ; c = A B a=BC; b=AC; c=AB . In △ A B C ′ ∠ B A C ′ = ( π − A − θ ) \triangle ABC' \angle BAC'=(π-A-\theta) . The Law of Sines for △ A B C ′ \triangle ABC' and △ B C A ′ \triangle BCA' gives: A ′ C ′ = A ′ B + B C ′ = s i n ( π − A − θ ) s i n A c + s i n θ s i n B a A'C'=A'B+BC'=\frac{sin(π-A-\theta)}{sinA}c+\frac{sin\theta}{sinB}a As s i n ( π − α ) = s i n α sin(π-\alpha)=sin\alpha and from the Law of Sines for △ A B C \triangle ABC a = c s i n A s i n C a=c\frac{sinA}{sinC} : k ( θ ) = A ′ C ′ c k(\theta)=\frac{A'C'}{c} k ( θ ) = s i n ( A + θ ) s i n A + s i n A . s i n θ s i n B . s i n C ; s i n ( x + y ) = s i n x . c o s y + c o s x . s i n y k(\theta)=\frac{\textcolor{#3D99F6}{sin(A+\theta)}}{sinA}+\frac{sinA.sin\theta}{sinB.sinC};\ \ \ \ \ \textcolor{#3D99F6}{sin(x+y)=sinx.cosy+cosx.siny} k ( θ ) = s i n A . s i n B . s i n C . c o s θ + s i n θ ( c o s A . s i n B . s i n C + s i n ² A ) s i n A . s i n B . s i n C k(\theta)=\frac{sinA.sinB.sinC.cos\theta+sin\theta(cosA.sinB.sinC+sin²A)}{sinA.sinB.sinC} k ( θ ) = c o s θ + s i n θ c o s A . s i n B . s i n C + s i n ² A s i n A s i n B s i n C k(\theta)=cos\theta+sin\theta\frac{cosA.sinB.sinC+sin²A}{sinAsinBsinC} Now let's make the term in the numerator a bit more 'cyclic' because it will be easier to work with it in that way: c o s A . s i n B . s i n C + s i n ² A = c o s A . s i n B . s i n C − c o s ² A + s i n ² A + c o s ² A ; s i n ² x + c o s ² x = 1 cosA.sinB.sinC+sin²A=cosA.sinB.sinC-cos²A+\textcolor{#3D99F6}{sin²A+cos²A};\ \ \ \ \ \textcolor{#3D99F6}{sin²x+cos²x=1} c o s A . s i n B . s i n C + s i n ² A = c o s A ( s i n B . s i n C − c o s A ) + 1 ; s i n x . s i n y = c o s ( x − y ) − c o s ( x + y ) 2 cosA.sinB.sinC+sin²A=cosA(\textcolor{#EC7300}{sinB.sinC}-cosA)+1;\ \ \ \ \ \textcolor{#EC7300}{sinx.siny=\frac{cos(x-y)-cos(x+y)}{2}} c o s A . s i n B . s i n C + s i n ² A = c o s A c o s ( B − C ) − c o s ( B + C ) − 2 c o s A 2 + 1 ; c o s A = − c o s ( B + C ) cosA.sinB.sinC+sin²A=cosA\frac{cos(B-C)-cos(B+C)-2\textcolor{#20A900}{cosA}}{2}+1;\ \ \ \ \ \textcolor{#20A900}{cosA=-cos(B+C)} c o s A . s i n B . s i n C + s i n ² A = c o s A c o s ( B − C ) + c o s ( B + C ) 2 + 1 ; c o s x + c o s y = 2 c o s x + y 2 c o s x − y 2 cosA.sinB.sinC+sin²A=cosA\frac{\textcolor{#EC7300}{cos(B-C)+cos(B+C)}}{2}+1;\ \ \ \ \ \textcolor{#EC7300}{cosx+cosy=2cos\frac{x+y}{2}cos\frac{x-y}{2}} c o s A . s i n B . s i n C + s i n ² A = c o s A . c o s B . c o s ( − C ) + 1 ; c o s ( − x ) = c o s x cosA.sinB.sinC+sin²A=cosA.cosB.\textcolor{#20A900}{cos(-C)}+1;\ \ \ \ \ \textcolor{#20A900}{cos(-x)=cosx} c o s A . s i n B . s i n C + s i n ² A = c o s A . c o s B . c o s C + 1 cosA.sinB.sinC+sin²A=cosA.cosB.cosC+1 If we let c o s A . c o s B . c o s C = p cosA.cosB.cosC=p and s i n A . s i n B . s i n C = q sinA.sinB.sinC=q , then k ( θ ) = c o s θ + p + 1 q s i n θ k(\theta)=cos\theta+\frac{p+1}{q}sin\theta . Note that k ′ ( θ ) = − s i n θ + p + 1 q c o s θ k'(\theta)=-sin\theta+\frac{p+1}{q}cos\theta and so k ( θ ) k(\theta) has an extremum (which is easily found to be a maximum) for k ′ ( θ 0 ) = 0 k'(\theta_0)=0 . Solving this equation yields t a n θ 0 = p + 1 q tan\theta_0=\frac{p+1}{q} and so our answer is (with p p and q q defined above): k m a x 2 = k 2 ( θ 0 ) = ( c o s θ 0 + t a n θ 0 s i n θ 0 ) 2 = s e c 2 θ 0 = 1 + t a n 2 θ 0 = 1 + ( p + 1 q ) 2 k^2_{max}=k^2(\theta_0)=(cos\theta_0+tan\theta_0sin\theta_0)^2=sec^2\theta_0=1+tan^2\theta_0=1+\left(\frac{p+1}{q}\right)^2 Now we have to find the values of p p and q q for the given values of the angles of the triangle which turns out to be just a matter of clever sequence of trigonometric transformations. p = c o s π 7 c o s 2 π 7 c o s 4 π 7 ; Multiply and divide by 8 s i n π 7 p=cos\frac{\pi}{7}cos\frac{2\pi}{7}cos\frac{4\pi}{7}\text{; Multiply and divide by }8sin\frac{\pi}{7} p = 2 ( 2 ( 2 s i n π 7 c o s π 7 ) c o s 2 π 7 ) c o s 4 π 7 8 s i n π 7 ; 2 s i n x c o s x = s i n 2 x p=\frac{2\left(2\left(\textcolor{#3D99F6}{2sin\frac{\pi}{7}cos\frac{\pi}{7}}\right)cos\frac{2\pi}{7}\right)cos\frac{4\pi}{7}}{8sin\frac{\pi}{7}};\ \ \ \ \ \textcolor{#3D99F6}{2sinxcosx=sin2x} p = 2 ( 2 s i n 2 π 7 c o s 2 π 7 ) c o s 4 π 7 8 s i n π 7 p=\frac{2\left(\textcolor{#3D99F6}{2sin\frac{2\pi}{7}cos\frac{2\pi}{7}}\right)cos\frac{4\pi}{7}}{8sin\frac{\pi}{7}} p = 2 s i n 4 π 7 c o s 4 π 7 8 s i n π 7 p=\frac{\textcolor{#3D99F6}{2sin\frac{4\pi}{7}cos\frac{4\pi}{7}}}{8sin\frac{\pi}{7}} p = s i n 8 π 7 8 s i n π 7 ; s i n ( π + π 7 ) = − s i n π 7 p=\frac{\textcolor{#20A900}{sin\frac{8\pi}{7}}}{8sin\frac{\pi}{7}};\ \ \ \ \ \textcolor{#20A900}{sin\left(\pi+\frac{\pi}{7}\right)=-sin\frac{\pi}{7}} ⇒ p = − 1 8 \Rightarrow p=-\frac{1}{8} Now note that p ′ = c o s π 7 c o s 2 π 7 c o s 3 π 7 = 1 8 = − p p'=cos\frac{\pi}{7}cos\frac{2\pi}{7}cos\frac{3\pi}{7}=\frac{1}{8}=-p . For q q : q = s i n π 7 s i n 2 π 7 s i n 4 π 7 ; s i n 4 π 7 = s i n 3 π 7 q=sin\frac{\pi}{7}sin\frac{2\pi}{7}\textcolor{#20A900}{sin\frac{4\pi}{7}};\ \ \ \ \ \textcolor{#20A900}{sin\frac{4\pi}{7}=sin\frac{3\pi}{7}} 8 q 2 = ( 2 s i n 2 π 7 ) ( 2 s i n 2 2 π 7 ) ( 2 s i n 2 3 π 7 ) ; 2 s i n 2 x = 1 − c o s 2 x 8q^2=\left(\textcolor{#3D99F6}{2sin^2\frac{\pi}{7}}\right)\left(\textcolor{#3D99F6}{2sin^2\frac{2\pi}{7}}\right)\left(\textcolor{#3D99F6}{2sin^2\frac{3\pi}{7}}\right);\ \ \ \ \ \textcolor{#3D99F6}{2sin^2x=1-cos2x} 8 q 2 = ( 1 − c o s 2 π 7 ) ( 1 − c o s 4 π 7 ) ( 1 − c o s 6 π 7 ) ; c o s ( π − x ) = − c o s x 8q^2=\left( 1-cos\frac{2\pi}{7}\right) \left( 1-\textcolor{#20A900}{cos\frac{4\pi}{7}}\right) \left( 1-\textcolor{#20A900}{cos\frac{6\pi}{7}}\right) ;\ \ \ \ \ \textcolor{#20A900}{cos\left(\pi-x\right)=-cosx} 8 q 2 = ( 1 + c o s π 7 ) ( 1 − c o s 2 π 7 ) ( 1 + c o s 3 π 7 ) 8q^2=\left(1+cos\frac{\pi}{7}\right)\left(1-cos\frac{2\pi}{7}\right)\left(1+cos\frac{3\pi}{7}\right) 8 q 2 = 1 − p ′ + ( c o s π 7 − c o s 2 π 7 + c o s 3 π 7 ) − ( c o s π 7 c o s 2 π 7 + c o s 2 π 7 c o s 3 π 7 − c o s 3 π 7 c o s π 7 ) 8q^2=1-p'+\left(cos\frac{\pi}{7}-cos\frac{2\pi}{7}+cos\frac{3\pi}{7}\right) - \textcolor{#D61F06}{\left(cos\frac{\pi}{7}cos\frac{2\pi}{7}+cos\frac{2\pi}{7}cos\frac{3\pi}{7}-cos\frac{3\pi}{7}cos\frac{\pi}{7}\right)} Let's denote the red expression as X X Using the identity c o s x . c o s y = c o s ( x + y ) + c o s ( x − y ) 2 cosx.cosy=\frac{cos(x+y)+cos(x-y)}{2} we get: X = c o s 3 π 7 + c o s π 7 + c o s 5 π 7 + c o s π 7 − c o s 4 π 7 − c o s 2 π 7 2 ; c o s x = − c o s ( π − x ) ) X=\frac{cos\frac{3\pi}{7}+cos\frac{\pi}{7}+\textcolor{#20A900}{cos\frac{5\pi}{7}}+cos\frac{\pi}{7}-\textcolor{#20A900}{cos\frac{4\pi}{7}}-cos\frac{2\pi}{7}}{2};\ \ \ \ \ \textcolor{#20A900}{cosx=-cos(\pi-x))} X = c o s 3 π 7 + c o s π 7 − c o s 2 π 7 + c o s π 7 + c o s 3 π 7 − c o s 2 π 7 2 X=\frac{cos\frac{3\pi}{7}+cos\frac{\pi}{7}-cos\frac{2\pi}{7}+cos\frac{\pi}{7}+cos\frac{3\pi}{7}-cos\frac{2\pi}{7}}{2} X = c o s π 7 − c o s 2 π 7 + c o s 3 π 7 X=cos\frac{\pi}{7}-cos\frac{2\pi}{7}+cos\frac{3\pi}{7} Substituting this new expression for X X in the last expression of 8 q 2 8q^2 we get: 8 q 2 = 1 − p ′ + ( c o s π 7 − c o s 2 π 7 + c o s 3 π 7 ) − ( c o s π 7 − c o s 2 π 7 + c o s 3 π 7 ) ; p ′ = 1 8 8q^2=1-\textcolor{#69047E}{p'}+\left(cos\frac{\pi}{7}-cos\frac{2\pi}{7}+cos\frac{3\pi}{7}\right) - \left(cos\frac{\pi}{7}-cos\frac{2\pi}{7}+cos\frac{3\pi}{7}\right);\ \ \ \ \ \textcolor{#69047E}{p'=\frac{1}{8}} 8 q 2 = 7 8 8q^2=\frac{7}{8} ⇒ q = 7 8 \Rightarrow q=\frac{\sqrt{7}}{8} Now all we have to do is to evaluate k m a x 2 k^2_{max} : k m a x 2 = 1 + ( p + 1 q ) 2 = 1 + ( 1 − 1 8 7 8 ) 2 = 8 k^2_{max}=1+\left(\frac{p+1}{q}\right)^2=1+\left(\frac{1-\frac{1}{8}}{\frac{\sqrt{7}}{8}}\right)^2=\fbox{8}

1 Helpful 1 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...