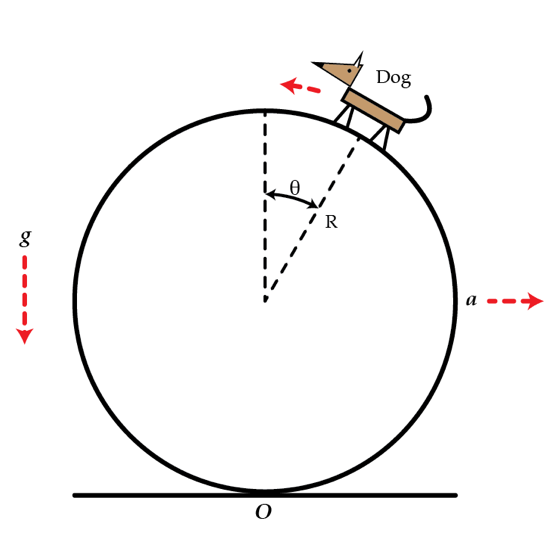
Circus dog

As the cylinder rolls without slipping, it is convenient to place the instantaneous axis of rotation at the point of contact between the ground and the cylinder.

According to the definition, $\tau=dL/dt=dL_{cyl}/dt+dL_{dog}/dt$

Let the mass of dog be $m$ and that of cylinder is $4m$ . We have $L_{cyl}=6mR^2\omega=6mRv$ and similarly $L_{dog}=mvR(1+\cos(\pi/6))$ (The dog performs only horizontal motion and $v$ represents the linear velocity.)

The time derivatives of angular momenta can be easily calculated. The only torque about the axis is due to the weight of the dog i.e. $mgR\sin(\pi/6)$ .

Hence, $\displaystyle mgR\sin(\pi/6)=6mRa+maR(1+\cos(\pi/6)$

$\displaystyle \Rightarrow a=\frac{g\sin(\pi/6)}{7+\cos(\pi/6)} \Rightarrow a=0.623 m/s^2$

Consider the forces on the dog (mass m): normal (N), friction (f1) and weight. Orienting the axes to coincide with the direction of acceleration gives:

$mg = N cos \theta + f1 sin \theta$ [equation A]

$ma = N sin \theta - f1 cos \theta$ [B]

Consider the dog and the cylinder as one object. The external forces on this object are the friction (f2) and the normal force from the floor, and the total weight. We have:

$f2 = 5 ma$ [C]

Consider the torques on the cylinder (radius R). Only frictional forces provide torque. Noting that, a = R alpha (no slipping), and that the moment of inertia of a uniform solid cylinder (mass m, radius R) about its central axis is given by $(1/2) mR^2$ , we have:

$f1 R - f2 R = (1/2)(4m)(Ra)$ [D]

Simplifying the previous equation:

$f1 - f2 = 2 ma$ [E]

From the previous equation and C:

$f1 = 7 ma$ [F]

Using C and F on B, and that $\theta = 30$ degrees, N can be solved in terms of ma. Substituting N and f1 in A, will allow us to cancel m, and express a in terms of g:

$a = g / (14 + \sqrt {3})$

We can put all the forces that act on the sphere, we'll use the Cartesian system:

x.i -> parallel to the floor y.j -> perpendicular to the floor

Now we can write the forces: We can use the draw of the problem to see the vectors

1) for the sphere

Friction force between the sphere and the floor (Fat_1)

Fat 1 = Fat 1.i

Friction force between the sphere and the dog

Fat 2 = Fat 2.cos(30).i - Fat_2.sin(30).j

Gravitational force

P = -4mg.j

Contact force between the sphere and the dog

N 2 = -N 2.sin(30) - N_2.cos(30)

The contact force between the sphere and the floor

N 1 = N 1.j

2) for the dog

The contact force between the dog and the sphere, from the third newton's law we get that the modulus of the forces are the same

N 2 = N 2.sin(30).i + N_2.cos(30).j

Gravitational force

p = -mg.j

Friction force between the sphere and the dog, from the third newton's law we get that the modulus of the forces are the same

Fat 2 = -Fat 2.cos(30).i + Fat_2.sin(30).j

Now we have to analize the resulting torque acting on the sphere:

Since the sphere is rotating with a w on the z direction of our referencial, we can conclude that

Torque = I.α = (1/2).α.M.R^2 = 2.α.mR^2 = (Fat 2 - Fat 1).R Where R is the cilinder's radius, α is the angular acceleration and I is the inertia momentum

But there is no slipping so we can say that v = wR -> a = αR Where a is the cilinder's center of mass' acceleration

So we have that

Fat 1 = Fat 2 - 2ma (eq.01)

Now we can apply the Newton's second law

For the sphere:

On the x axis

Fat 1 + Fat 2.cos(30) - N_2.sin(30) = 4ma

Substituting Fat_1 from the (eq.01) we have that

Fat 2 = (N 2 + 12ma)/(sqrt(3) + 2) (eq.02)

Now we analize the dog

In the x axis

N 2.sin(30) - Fat 2.cos(30) = ma

Fat 2 = N 2(sqrt(3)/3) - 2ma(sqrt(3)/3) (eq.03)

Substituting Fat_2 from the (eq.02) on (eq.03) we get that

N_2 = ma(7.sqrt(3) + 2) (eq.04)

Now on the y axis

Fat 2.sin(30) + N 2.cos(30) = mg

Substituting Fat_2 we get that

N_2 = (mg.sqrt(3) + ma)/2

Now we subistitute N_2 from the (eq.04)

We get that

a = g/(14 + sqrt(3)) = 0.62 m/s^2

the dog must be having just the horizontal acceleration a as same as the cylinder and also 0 vertical acceleration. Thus taking normal force acting between dog and cylinder as N and corresponding friction as f1 , also friction force from ground on cylinder as f2 resp. we get by writing force eqn. for dog in horizontal and vertical direction and on cylinder in horizontal direction resp. Nsin30-f1cos30=ma.....(1) Ncos30+f1sin30=mg.....(2) f1cos30+f2-Nsin30=4ma...(3) Also writing torque eqn. and applying condn. for pure rolling, (f1-f2)=4ma/2......(4) thus solving above eqns. a=0.62m/s^2

This problem can be easily solved by looking at the dog-cylinder system as a whole. The only external torque with respect to the point $O$ is $\tau=m g R \sin\theta$ where $m$ is the mass of the dog and $R$ the radius of the cylinder. Now, the angular momentum with respect to point $O$ can be written as $L=L_{cylinder}+ L_{dog}$ The angular momentum of the cylinder with respect to the point $O$ is just $L_{cylinder}= I_{0} \omega= (\frac{M R^{2}}{2}+ MR^{2}) \omega=\frac{3}{2}MR^{2} \omega$ where $M$ is the mass of the cylinder. Here, we made use of the Parallel Axis Theorem. The angular momentum of the dog is $L_{dog}=m v R (1+\cos\theta).$ Since the the cylinder rolls without slipping we have that $v=\omega R$ . Thus, we obtain the total angular momentum of the dog-cylinder system $L= \left(\frac{3}{2}M+ m (1+\cos\theta)\right) R v$ Since $\tau=\frac{d L}{dt}$ and $a=\frac{dv}{dt}$ we find that $a= \frac{mg \sin \theta}{\frac{3}{2}M+m(1+\cos\theta)}= \frac{g \sin\theta}{7+\cos\theta}=0.62~\mbox{m/s}^{2}.$

the dog must be having just the horizontal acceleration a as same as the cylinder and also 0 vertical acceleration. Thus taking normal force acting between dog and cylinder as N and corresponding friction as f1 , also friction force from ground on cylinder as f2 resp. we get by writing force eqn. for dog in horizontal and vertical direction and on cylinder in horizontal direction resp. Nsin30-f1cos30=ma.....(1) Ncos30+f1sin30=mg.....(2) f1cos30+f2-Nsin30=4ma...(3) Also writing torque eqn. and applying condn. for pure rolling, (f1-f2)=4ma/2......(4) thus solving above eqns. a=0.62m/s^2