Jee Mechanics
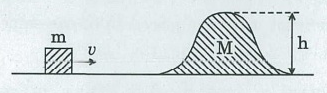
A small block of mass and a smooth irregular shaped block of mass , both free to move, are placed on a smooth horizontal plane. Find the minimum velocity to be imparted to the smaller block so that it reaches the highest point of the large block.
Details and Assumptions: , , , and the acceleration due to gravity .
The problem is not original.
The answer is 20.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The initial energy of the system is the kinetic energy of the small block m , E 0 = 2 1 m v 2 . After the block m hits the irregular shaped block M , part of the initial kinetic energy is converted to moving the two blocks m + M with a velocity v 1 , E v . Another part is converted to potential energy for block m to move vertically up block M , E p . The minimum v is the one that block m reaches the highest point of block M and stops or when
E 0 2 1 m v 2 2 1 m v 2 2 1 m v 2 v 2 ⟹ v = E v + E p = 2 1 ( m + M ) v 1 2 + m g h = 2 1 ( m + M ) ( m + M m v ) 2 + m g h = 2 1 × m + M m 2 v 2 + m g h = m + M m v 2 + 2 g h = M 2 g h ( m + M ) = 1 2 2 ⋅ 1 0 ⋅ 1 2 ( 8 + 1 2 ) = 2 0 By conservation of momentum: m v = ( m + M ) v 1 ⟹ v 1 = m + M m v Multiply both sides by m 2 Rearrange