Calculate the bullet speed
One way of measuring a projectile's speed is by using a ballistic pendulum , as shown below.
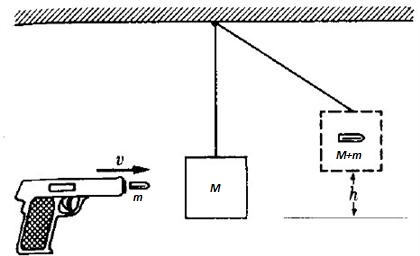
This pendulum is a piece of wood of mass M , suspended by a fine, lightweight wire. Initially, the pendulum is at rest. A bullet of mass m horizontally strikes the piece of wood and gets stuck in it, causing the pendulum to lift up at height h .
If the mass of the pendulum is M = 4 kg , the bullet's mass is m = 9 . 7 g , and after impact they lift up to h = 1 9 cm , what is the initial speed (in m/s ) of the bullet (to the nearest integer)?
Details and Assumptions:
- The gravitational acceleration is g = 9 . 8 m/s 2 .
The answer is 798.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
When I did the problem I rounded at the last step and got 797. I noticed if I did the significant figures at each step I would get 798. Can you kindly remind me which is right or if the answer should have a plus or minus 1 error bar on it.
Thanks!
Log in to reply
There is no plus or minus error involved . I'm pretty much sure that 798 is the right answer . The only way you could get 797 is by taking the velocity of the pendulum after impact with 2 decimal places , instead of the whole number .
The main insight comes from realizing that the collision between the bullet and the block is completely plastic, therefore the maximum possible amount of energy is lost during the collision. During the collision, we have:
m b v b = ( m b + M ) v f
Due to conservation of energy:
2 1 ( m b + M ) v f 2 = ( m b + M ) g h
And so we have:
2 1 v f 2 = g h ⇒ 2 ( m b + M ) 2 m b 2 v b 2 = g h ⇒ v b = m b 2 2 g h ( m b + M ) 2 = 2 g h m b m b + M = 2 ( 9 . 8 1 ) ( 0 . 1 9 ) 0 . 0 0 9 7 4 . 0 0 9 7 ≈ 7 9 8 m / s
Relevant wiki: Analyzing inelastic collisions
Consider v 0 = the initial speed of the bullet , and v = the speed of the pendulum after the impact . If the bullet remains stuck in the pendulum , then we have to deal with a plastic clush .
From momentum consevation we get m ⋅ v 0 = ( m + M ) ⋅ v .
From the energy conservation of the pendulum we get ( m + M ) ⋅ 2 v 2 = ( m + M ) ⋅ g ⋅ h .
From the two equations we can find v 0 , which is 7 9 8 m / s