Climbing The Staircase
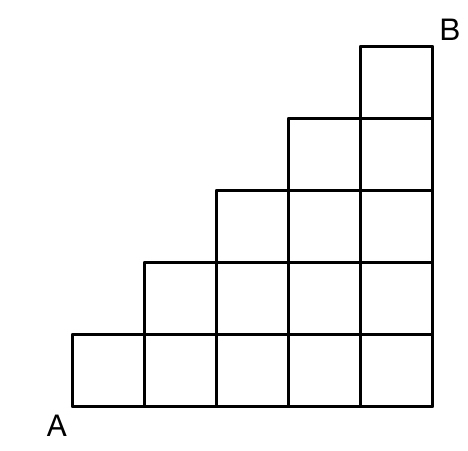
How many paths are there from A to B that only move up or right?
The answer is 132.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
With n "nodes" along the base and right side, the number of paths is the Catalan number
C ( n ) = n ! ( n + 1 ) ! ( 2 n ) ! .
In this case there are C ( 6 ) = 6 ! 7 ! 1 2 ! = 1 3 2 pathes.
Log in to reply
Yes! How can we immediately relate it to the catalan numbers ?
@Chung Kevin The Catalan number is directly involved because one cannot go up without having gone right.
It must be 1 instead of 2 at 3rd bottom place from left.
Log in to reply
It must be 1 in bottom row everywhere.
A simple but time taking recursion -
def P(i, j):
if i == 0 or j == 0: return 1
else:
if(j <= i): return (P(i - 1, j) + P(i, j - 1))
else: return P(i, j - 1)
Here P ( i , j ) is the number of valid paths from ( 0 , 0 ) to ( i , j ) .
For such problems, there is always the trivial approach of listing out the number of ways to reach each vertex, by proceeding form the start point and moving right / up. This may be tedious, but it works everytime.
There is actually a pattern to this staircase. Can you find the generalized answer?