Having An Electric Time
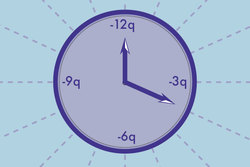 A clock face has charges
−
q
,
−
2
q
,
−
3
q
,
−
4
q
,
…
,
−
1
2
q
that are fixed at a position of the corresponding numerals on the dial. The clock hands do not disturb the net field due to point charges. If the
hour
hand were to point in the direction of the electric field, what time would it say?
A clock face has charges
−
q
,
−
2
q
,
−
3
q
,
−
4
q
,
…
,
−
1
2
q
that are fixed at a position of the corresponding numerals on the dial. The clock hands do not disturb the net field due to point charges. If the
hour
hand were to point in the direction of the electric field, what time would it say?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
8 solutions
I used the same logic. Symmetry works well here, plus we end up with six -6q charges at the end which makes it easier. From 7:00 - 12:00, the average value is 9:30. Hence the answer.
thanks
superb .. thnks
good logic there :)
Use symmetry... and its all easy.
The field of the Opposite directional charges demolish themselves . Its like -12-(-6)=-6 .So -1,-2,-3,-4,-5,-6 becomes 0 and -7,-8,-9,-10,-11,-12 becomes -6 . Next , now they are all equally charged and same direction . so find the middle number between 7 and 12 . its 9.30 . Those were all negative charges , so direction towards 9.30 . If they were +ve , it would be opposite to 9.30 ; ie 3.30 :)
nice
Interesting question! Consider the charges q i be analogous to mass, the problem is solve for the center of 'charge' ( x ˉ , y ˉ ) from the center of the clock ( 0 , 0 ) as follows:
x ˉ = 1 2 + 6 1 2 + 6 ( 0 ) + 1 + 5 + 7 + 1 1 1 + 5 − 7 − 1 1 cos 6 0 ∘ + 2 + 4 + 8 + 1 0 2 + 4 − 8 − 1 0 cos 3 0 ∘ + 3 + 9 3 − 9 ( 1 )
= − 4 1 − 4 3 − 2 1 = − 4 1 ( 3 + 3 )
Similarly, we find that y ˉ = 3 1 .
Let tan θ = x ˉ y ˉ ⇒ θ = − 1 5 . 7 ∘ ⇒ the hour hand pointed to 9 : 3 0 .
- draw diagram
- use vector method
- you will get answer
ask
check the direction of electric field ,thats it
This is a nice but easy problem from DCP.Innovative problem.
by symmetry argument we ultimately end up with two vectors along 9 direction and 12 direction, but the former is longer than the latter thus the resultant is slightly below the central position which has to be 9:30.
As the radius is constant in all cases , we can assume the the net charge is concentrated at one place i.e. center of charge ( just like center of mass). And at that point the net electric field is acting.
Since the radius is constant, the component of the electric field in each direction is proportional to the charge. Thus, for some constant k and for all 1 ≤ i ≤ 1 2 , the electric field component towards numeral i will be equal to k i .
We can combine the components in opposite directions. In the direction of numeral 12, the component is 1 2 k − 6 k = 6 k . In the direction of numeral 11, it is 1 1 k − 5 k = 6 k . Similarly for the component in the direction of numerals 10, 9, 8, and 7. Thus we have that the electric field is the sum of six components, each of magnitude 6 k , in the directions of numerals 7, 8, 9, 10, 11, and 12. By symmetry, the net electric field will point halfway between 9 and 10, or at 9 : 3 0 .