Close approach -- nested -- perhaps, not closed form. (Try 2).

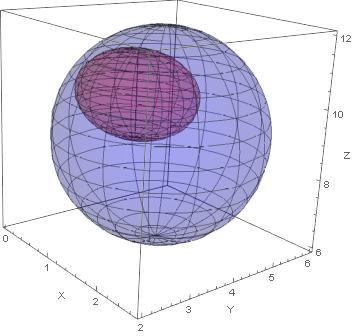
The objects are described in 2-dimensional spherical surface coordinates (similar to latitude and longitude) to give Cartesian (x,y,z) coordinates. $0\leq\theta\leq\pi$ . $0\leq\phi\leq 2\pi$ . The objects are just the described surfaces. Therefore, the objects are not touching. One is inside the other.

$\text{object1}(\theta,\phi)=\left\{\frac{5}{6} \sin (\theta ) \cos (\phi )+\frac{5}{4},\sin (\theta ) \sin (\phi )+\frac{7}{2},\frac{6 \cos (\theta )}{5}+\frac{51}{5}\right\}$

$\text{object2}(\theta,\phi)=\left\{\frac{4}{3} \sin (\theta ) \cos (\phi )+\frac{4}{3},2 \sin (\theta ) \sin (\phi )+4,3 \cos (\theta )+9\right\}$

What is $100\times\text{the minimum distance}$ ? To help you, the multiplied answer is between 0 and 20.

This problem is difficult because of the lack of a closed form and that the gradient of the distance is very small.

Clarification: Previous version of problem omitted a square root at the very end. I apologize.