Closer to Center (Corrected)

Label the diagram as follows:

The coordinates of the centroid are $G(\frac{1}{3}(A_x + B_x + C_x), \frac{1}{3}(A_y + B_y + C_y)) = G(1, \frac{1}{3})$ .

$AC$ is on the line $x - y = 0$ and $AB$ is on the line $y = 0$ .

The locus of points that are equidistant from a point and a line is a parabola , so the curve through $D$ and $E$ is a parabola with a focus of $G(1, \frac{1}{3})$ and a directrix of $y = 0$ , and using $\frac{(ax + by + c)^2}{a^2 + b^2} = (x - f_1)^2 + (y - f_2)^2$ its equation is $\frac{(0 + y + 0)^2}{0^2 + 1^2} = (x - 1)^2 + (y - \frac{1}{3})^2$ , which solves to $y = \frac{3}{2}x^2 - 3x + \frac{5}{3}$ .

The curve through $D$ and $F$ is a parabola with a focus of $G(1, \frac{1}{3})$ and a directrix of $x - y = 0$ , and using $\frac{(ax + by + c)^2}{a^2 + b^2} = (x - f_1)^2 + (y - f_2)^2$ its equation is $\frac{(x - y + 0)^2}{1^2 + 1^2} = (x - 1)^2 + (y - \frac{1}{3})^2$ , which solves to $y = -x + \frac{2}{3} + \frac{2}{3}\sqrt{6x - 4}$ .

The parabolas $y = \frac{3}{2}x^2 - 3x + \frac{5}{3}$ and $y = -x + \frac{2}{3} + \frac{2}{3}\sqrt{6x - 4}$ intersect at an $x$ -coordinate of $D_x = \frac{1}{3}(2 + \sqrt{2} - 2\sqrt{\sqrt{2} - 1})$ .

The area of the region closer to the centroid $G$ is therefore:

$A = 2\int_{D_x}^{1} [(-x + \frac{2}{3} + \frac{2}{3}\sqrt{6x - 4}) - (\frac{3}{2}x^2 - 3x + \frac{5}{3})] dx = \frac{1}{27}(-31 + 20\sqrt{2} + 8\sqrt{2(\sqrt{2} - 1)}) \approx \boxed{0.169}$ .

Here is a rough outline of my solution:

1) Do a double integral to find the centroid location. This is essentially an area-weighted average of the $(x,y)$ coordinates. This could have been a single integral, but Step 2 requires a double integral anyway, so it made sense to have a common approach.

2) Having found the centroid, do another double integral to accumulate area that is closer to the centroid than to any side. To accomplish this, I used the formula for the distance from a point to a line segment found at Wolfram Mathworld (Equation 14).

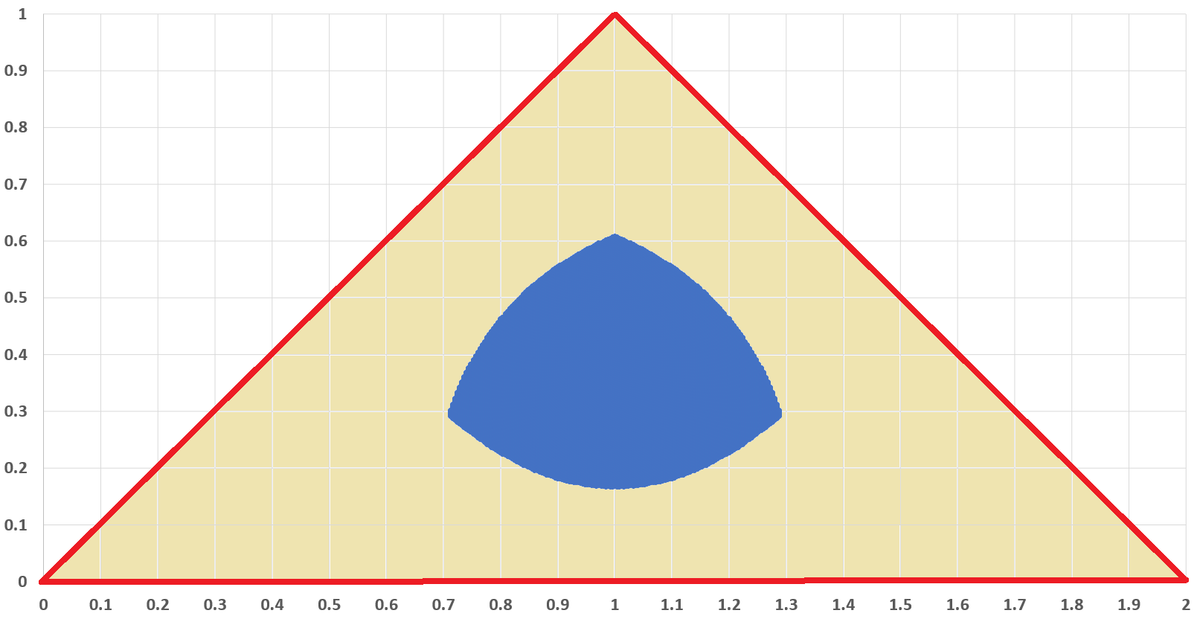
The graphic below shows the region of interest in blue. It is $16.9 \%$ of the total triangle area.

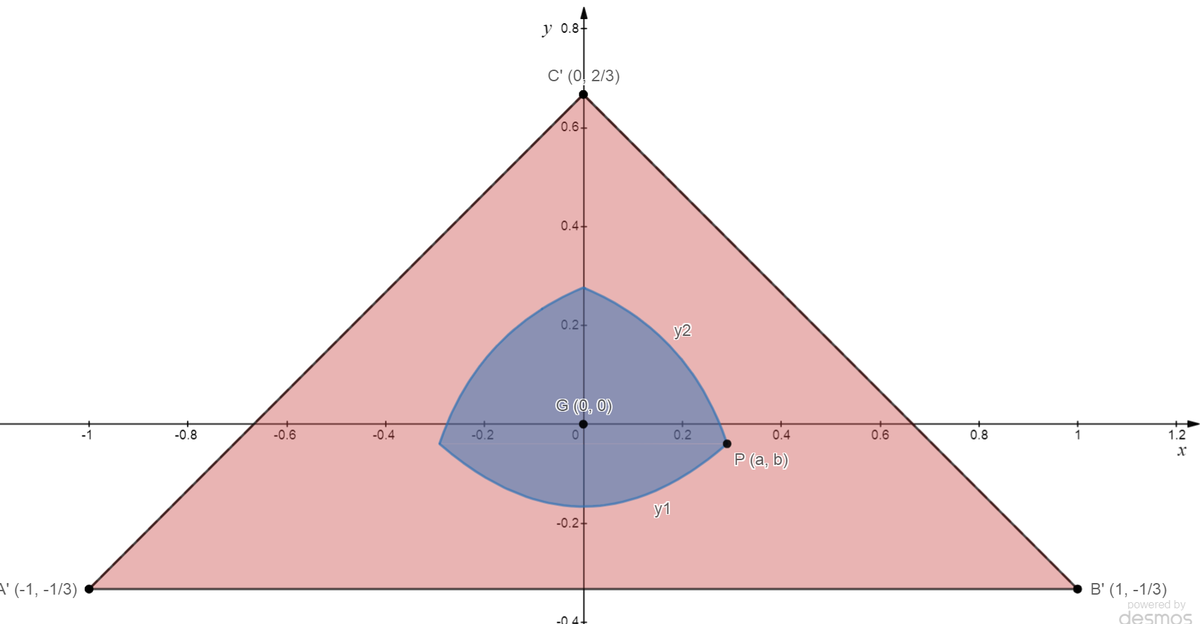
The locus of points which are equidistance from the centroid and an edge straight line is a parabola, where the centroid is the focus point $F (x_f, y_f)$ and the edge straight line $ax+by+c = 0$ is the directrix. And the equation of the parabola is given by ( reference ):

$\frac {(ax+by+c)^2}{a^2+b^2} = (x-x_f)^2 + (y-y_f)^2$

To make the calculations easy, we set $(x_f, y_f) = (0,0)$ or we move $G(x_g, y_g)$ to $G'(0,0)$ . Since $x_g = \dfrac {x_a+x_b+x_c}3 = \dfrac {0+2+1}3 = 1$ and $y_g = \dfrac {y_a+y_b+y_c}3 = \dfrac {0+0+1}3 = \dfrac 13$ , then $A' = \left(x_a-1, y_a - \dfrac 13\right) = \left(-1,- \dfrac 13\right)$ , $B'= \left(1,- \dfrac 13\right)$ , and $C' = \left(0, \dfrac 23\right)$ . Then the equation of the three parabolas are:

$\begin{cases} 6y = 9x^2 - 1 & ...(1) \ \rm bottom \\ 9 (x-y)^2+12 (x+y)-4 = 0 & ...(2) \ \rm right \\ 9 (x+y)^2-12 (x-y)-4 = 0 & ...(3) \ \rm left \end{cases}$

The region shaded blue is the part of the triangle which is nearer to the centroid $G$ than an edge. Since the area is symmetrical about the y-axis, we can find the area of the right half and then multiply it by $2$ .

From $(1)$ , we get $y = \dfrac 32 x^2 - \dfrac 16 = y_1$ and from $(2)$ , $y=x+\dfrac {2\sqrt{2-6x}}3 - \dfrac 23 =y_2$ . Let parabolas $y_1$ and $y_2$ meet at $P(a,b)$ . From $y_1 = y_2$ , $a = \dfrac {1-\sqrt 2 + 2\sqrt{\sqrt 2-1}}3$ . And the area of the blue region:

$\begin{aligned} A & = \int_0^a (y_2 - y_1) \ dx \\ & = 2 \int_0^a \left(x + \frac {2\sqrt{2-6x}}3 - \frac 12 - \frac 32 x^2\right) dx \\ & = \int_0^a \left(- 3x^2 + 2x - 1 + \frac {4\sqrt{2-6x}}3\right) dx \\ & = - x^3 + x^2 - x - \frac {4(2-6x)^\frac 32}{27} \bigg|_0^a \\ & = - a^3 + a^2 - a - \frac {4(2-6a)^\frac 32}{27} + \frac {8\sqrt 2}{27} \\ & = \small \frac {17+4\sqrt 2 - 16\sqrt{\sqrt 2 -1} - 8\sqrt{2(\sqrt 2 -1)}-16\sqrt{\sqrt 2 - 2\sqrt{\sqrt 2 -1}}+16\sqrt{4-2\sqrt 2 + 4\sqrt{\sqrt 2 -1}-4\sqrt{2(\sqrt 2-1)}}}{27} \\ & \approx 0.169100334 \end{aligned}$

Since the area of $\triangle ABC = 1$ , $\dfrac A{[ABC]} = A \approx \boxed{0.169}$ .

My approach is similar to other people's but what I did is I considered only the left half of the triangle (due to symmetry). Then I drew the bisector of angle A, which splits the half-triangle in 2 regions (the bisector is the line, all points of which are equidistant to the corresponding sides). For the upper one the closest triangle side is AC and for the lower one - it is AB. For each region I found the curve, where all points are equidistant to G and to the corresponding side. Then I found the intersection point of these two curves (which obviously lies on the bisector) and then did two integrals from that point to x=1. The sum of the resulting areas is the left half of the desired area, so I multiplied this area by 2 and got approximately 0.169. Since the area of the triangle is 1, the answer is $\frac{0.169}{1}=0.169$ .