Cloudy day 2
Thinner clouds are white and shiny all over; thick clouds are shiny on the top and dark at the bottom. This effect is caused by incident sunlight scattering off of water droplets in the cloud. Since the sunlight is incident from the top, less light makes it all the way through the cloud to be scattered into our eyes, resulting in a darker bottom.
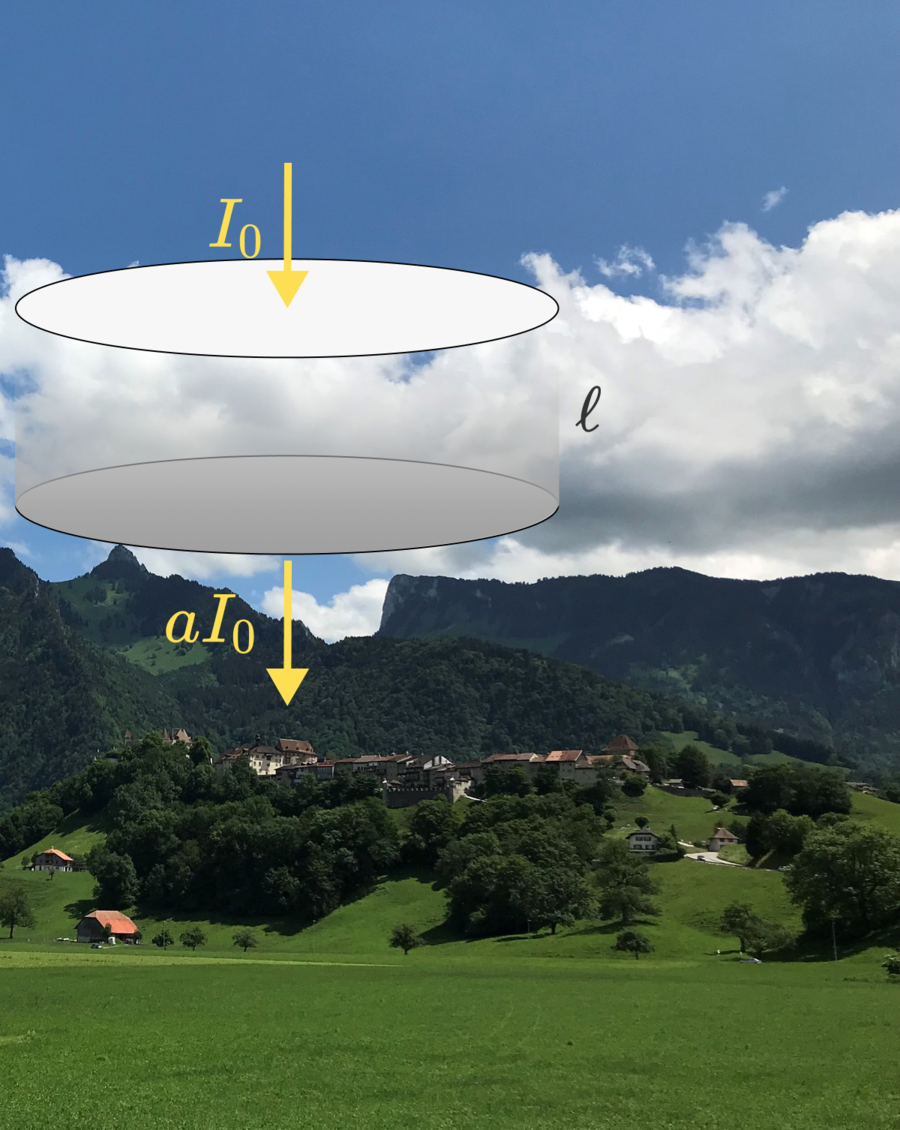
Suppose that the water droplets in the cloud are in diameter and there are about droplets in a cubic centimeter of cloud material. Sunlight with intensity is incident from above the cloud, and when light hits a droplet, it is scattered in a random direction with no loss of energy.
What fraction of the incident sunlight is coming out at the bottom of a -thick cloud in the form of scattered light? Give your answer rounded to three decimal places.
Hint: The scattering of light through a cloud is much like the scattering that occurs on ground level on a foggy day . You may also find it useful to try treating the propagation of the scattered light as a diffusion problem.
The answer is 0.1578.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
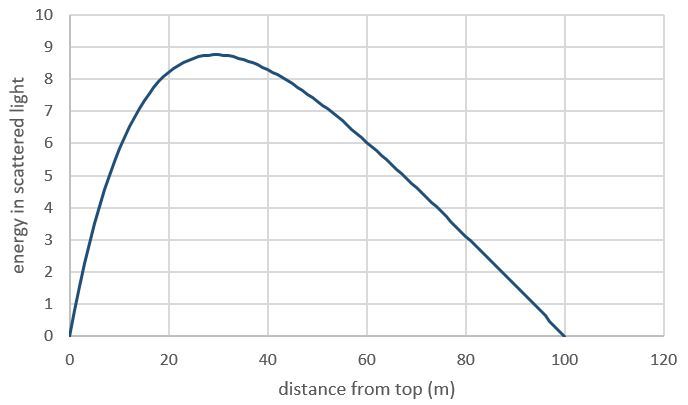
As the direct sunlight passes through the cloud its energy is constantly converted into the scattered light. This creates an energy density inside the cloud, in the form of scattered light. The energy of the scattered light will flow from the higher density to the lower density and eventually it will leave at the top or at the bottom of the cloud. In the steady state the energy deposited inside the cloud will be equal to the energy leaving the cloud.
Due to the assumptions of large planar surfaces the energy density will depend only on the distance from the top of the cloud, e = e ( z , t ) (in the steady state there is no time dependence, either, but for the intermediary steps of the calculation we keep it). The rate of energy deposition in the cloud is proportional to the intensity of the sunlight, W = Δ e / Δ t = μ I 0 e − μ z , where μ = 1 / λ , and λ = 1 5 . 9 m , as determined in the foggy day problem. The energy flow is proportional to the gradient of the energy density, j = − D ∂ z ∂ e . Energy conservation requires that
∂ t ∂ e = − ∂ z ∂ j + W or
∂ t ∂ e = D ∂ z 2 ∂ 2 e + W .
Here D is a constant that is somehow related to the mean free path λ , but the actual relationship is not important, because at the end the result will not depend on D . Since we look for the steady state, ∂ t ∂ e = 0 , and
∂ z 2 ∂ 2 e = − D I 0 μ e − μ z .
By integrating this equation we find the solution in the form of e = − μ D I 0 e − μ z + B z + C .
The constants B and C are determined from the boundary conditions: The energy density on the top and bottom of the cloud is zero, since the light reaching these surfaces will immediately leave the cloud. Therefore e ( z = 0 ) = 0 and e ( z = ℓ ) = 0 , where ℓ is the thickness of the cloud. These conditions yield C = I 0 / μ D and B = − μ D ℓ I 0 ( 1 − e − μ ℓ ) . The final form of the energy distribution is
e = μ D I 0 [ 1 − e − μ z − ℓ z ( 1 − e μ ℓ ) ] .
This distribution is shown in the first Figure below, for I 0 = 1 and D = 1 .
The flow of energy is
j = − D ∂ z ∂ e = I 0 [ − e − μ z + μ ℓ 1 ( 1 − e − μ ℓ ) ]
As noted before, this is independent of the parameter D . The second graph shows the energy flow.
The energy flow at the bottom of the cloud is 0 . 1 5 7 8 I 0 in the positive direction (downwards). Therefore the answer is 16%. The energy flow at the top of the cloud is negative (upwards), and its value is 0 . 8 4 0 3 I 0 . There is a very small energy flow left in the direct sunlight, 0 . 0 0 1 9 I 0 .
In general, the thicker is the cloud, the closer is to 100% the energy flow from the top. For a thin cloud the opposite is happening, the energy of the scattered light is about the same at the top and the bottom. For ℓ = 1 0 m the energy flow at the top is 26% of the incident intensity, the (scattered) energy flow at the bottom is 21% and 53% of the light remains in the undisturbed direct sunlight.