Cocentric Circles and Probability
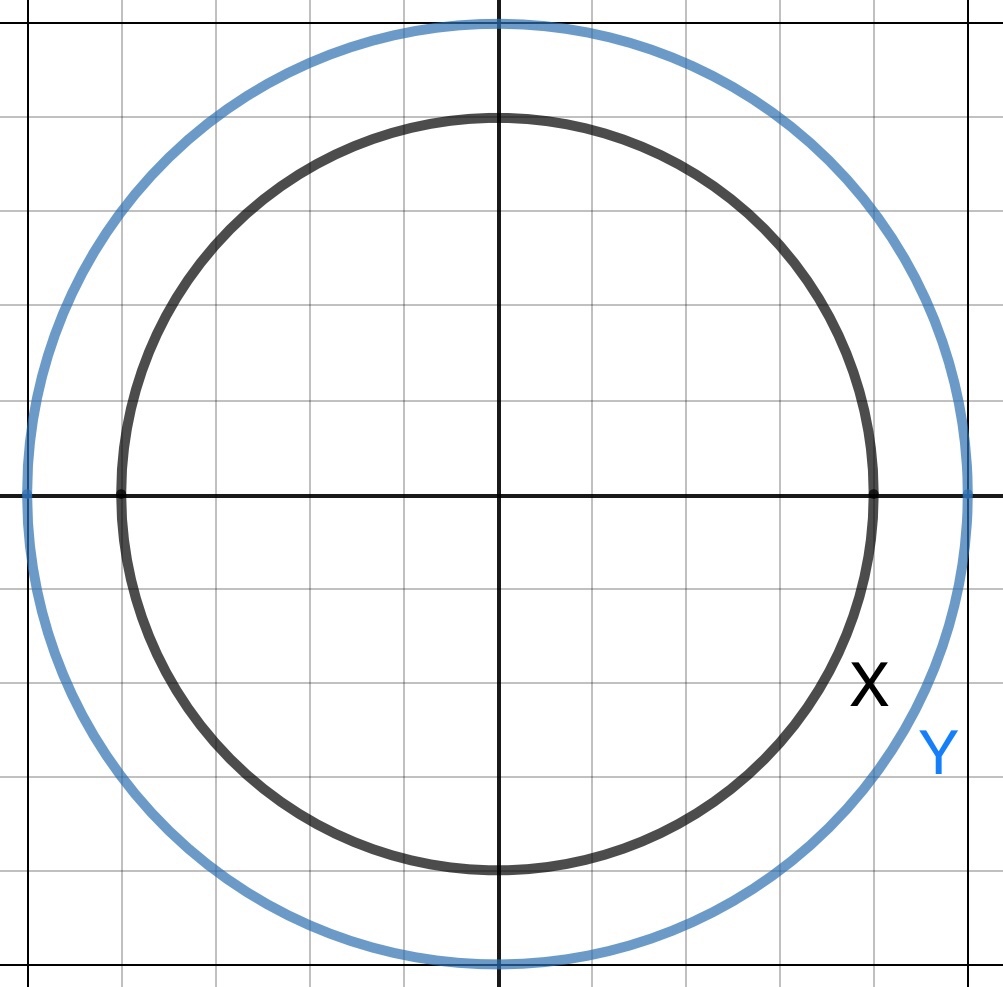
Two concentric circles and are drawn below, the radii of which are 4 and 5, respectively.
Now, consider the following differently sized equilateral triangles that has two vertices on and the third vertex on . Then, let denote the product of the side lengths of these two equilateral triangles.
If another concentric circle has a radius of what is the probability that a point selected uniformly at random in falls outside of i.e. falls within the ring formed by and
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
For simplicity since the triangle can rotate along the circles, we can consider the version of the triangle with C on the y -axis:
With:
x C = 0 , y C = 5
x A = − x B , y A = y B
Also, since A and B lie on X :
x A 2 + y A 2 = x B 2 + y B 2 = 1 6
So, we can say that A B = A C :
( x A − x B ) 2 + ( y A − y B ) 2 = ( x A − 0 ) 2 + ( y A − 5 ) 2
x A 2 + y A 2 + x B 2 + y B 2 − 2 x A x B − 2 y A y B = x A 2 + y A 2 − 1 0 y A + 2 5
Since x A 2 + y A 2 = x B 2 + y B 2 = 1 6 :
3 2 − 2 x A x B − 2 y A y B = 1 6 − 1 0 y A + 2 5
Since x A = − x B , y A = y B :
2 x A 2 − 2 y A 2 = − 1 0 y A + 9
Since x A 2 = 1 6 − y A 2 :
3 2 − 4 y A 2 = − 1 0 y A + 9
4 y A 2 − 1 0 y A − 2 3 = 0
So:
y A = 4 5 ± 3 1 3
Which leads to:
x A = − 1 6 1 1 4 ± 3 0 1 3
Each possible side will be l = x B − x A = − 2 x A , for each different x A :
l 1 = 2 1 6 1 1 4 + 3 0 1 3
l 2 = 2 1 6 1 1 4 − 3 0 1 3
r will be equal to l 1 ⋅ l 2 :
r = 9
So, the probability will be the area outside Y but within Z divided by the area of the whole Z :
p = π 9 2 π 9 2 − π 5 2
p = 8 1 5 6