Cody's "Angry LADIES" ! ....not birds....
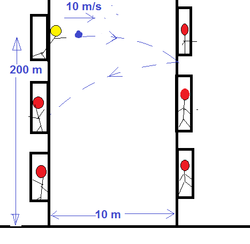 Cody (yellow) threw a
horizontally, as shown in the pic with velocity
for the
.
Cody (yellow) threw a
horizontally, as shown in the pic with velocity
for the
.
The point from where he throws it is above the ground.
The two buildings in the pic are apart. His chocolate strikes the opposite building (of course the lady doesn't get it) and at the very instant, all ladies close their windows. So his chocolate falls on the ground.
If the chocolate's speed is not affected by the collision with the building, how many times does the chocolate strike the walls of those buildings before it reaches the ground ?
Details and assumptions
Acceleration due to gravity
Cody's chocolate undergoes smooth collisions, it doesn't change the speed by the collision . The only force acting is gravity.
You have to find the number of times chocolate hits the walls , i.e. after those many collisions, before the next one, it will hit the ground.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The displacement along Y axis is − 2 0 0 m . Initial velocity along Y axis is 0.
S y = − 2 0 0 = u t − 2 g t 2 ... here u = 0 and g = 1 0
t 2 = 4 0 ⟹ t = 4 0 s e c o n d s
Acceleration along X axis is 0, and initial velocity is 10m/s as given.
Observe that if the walls were not there, the chocolate would have gone S x = u t + 2 a t 2 = 1 0 t = 1 0 4 0 m
Here in this case, according to given conditions of collision, note that if you unfold that path, it is same as the path without walls, hence here , the horizontally Distance covered (not displacement) is same as 1 0 4 0
Thus the chocolate moved horizontally a distance of 1 0 4 0 m during the motion and as the distance between walls is 1 0 m , the number of times it's path is changed, i.e. it hits the wall is
⌊ 1 0 1 0 4 0 ⌋ = ⌊ 4 0 ⌋ = 6
Thus it hits the walls 6 times and , before it could hit the wall 7th time, it reaches the ground.