Coin Grab
You have in front of you the following 4 boxes of coins:
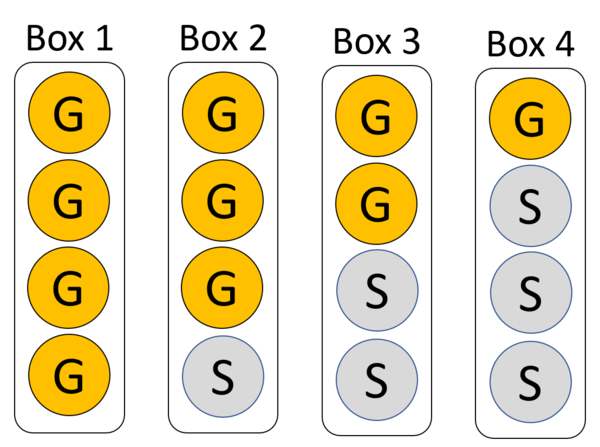
You are blindfolded, the boxes are randomly shuffled. You are instructed to select a box, and select two coins. What is the probability the second coin you've selected is silver?
The probability of the second coin being silver is given by P = b a , where a and b are positive coprime integers
Enter your answer as a + b .
Inspiration .
As always there is a good chance I've stepped outside of my understanding...if that is the case please report!
The answer is 11.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Ask and Mark shall provide! Its funny that I tried to make the problem harder than the "inspiration" for it, and I made it easier ( if one understands probability I suppose - which I apparently do not ).
Thank you for the solution ( maybe someday this notion will stick )!
I imagined the two possible cases for drawing a second silver coin:

For the first Draw:
P ( S ) = 4 1 ( 0 + 4 1 + 2 1 + 4 3 ) = 8 3
P ( G ) = 1 − P ( S ) = 8 5
I treated each independent case as if they happened. Thus, the probability of the second draw being silver depends on the state of the first draw.
P ( 2nd Draw S ) = P ( S ) ⋅ P ( S ∣ S ) + P ( G ) ⋅ P ( S ∣ G )
P ( S ∣ S ) = 6 0 ⋅ 0 + 6 1 ⋅ 0 + 6 2 ⋅ 3 1 + 6 3 ⋅ 3 2 = 9 4
P ( S ∣ G ) = 1 0 4 ⋅ 0 + 1 0 3 ⋅ 0 + 1 0 2 ⋅ 3 2 + 1 0 1 ⋅ 1 = 3 1
Finally:
P ( 2nd Draw S ) = P ( S ) ⋅ P ( S ∣ S ) + P ( G ) ⋅ P ( S ∣ G ) = 8 3 ⋅ 9 4 + 8 5 ⋅ 3 1 = 8 3
Given @Mark Hennings solution, I award myself a "C" for effort!
(since you're at the "solution to follow" stage) is there an intuitive reason why the probability is the same as that of just picking a single silver coin out of the whole selection? (There are six silver coins out of sixteen in total)
Log in to reply
Hi Chris. You'd probably be the one I'd ( of us ) ask if there is an elegant way of doing it. I used conditional probabilities, so I don't have an intuitive answer. If you do or come up with something, please feel free to share ( I always enjoy smacking my hand against my head in duh moments )!
sorry i am still confuse, after first draw a coin is picked up randomly, Therefore, shouldn't we calculate the probability of the coins after being picked up randomly from each box ?
Log in to reply
That is what I have done in my solution. It works, but it would get really messy if I had asked draw 3, what is the likelihood of the 4th being sliver, etc... See the solution of Mark Henning's for what should be done. It bypasses the whole conditional probability argument and it would work right up to the last draw I believe.
this problem says select one box for two coin. Isn't this a combination problem that you need to pick two coins from one box? so for total there would be 4 2C4=24. for each there would be 3 for second box (first coin is G got three possibility), 2 2 for third ( first G first S first G second S and second G first S and second G second S), 6 for forth box (G1 to S1, S2, S3 and S1,S2,S3 pick 2 out of three)= 13/24?
Log in to reply
Sure, you can look at it in this way too! But you must be careful about keeping the method of counting consistent.
There are 4 Boxes from which to chose, and for each of those there are 4 choices for the first coin and 3 choices for the second coin ( imagine for Box 1 having G 1 , G 2 , G 3 , G 4 etc...)
The number of ways to select two coins is given by:
4 ⋅ 4 ⋅ 3 = 4 8
For Box 1 ( second coin silver )
N 1 = 0
For Box 2 ( second coin silver ):
N 2 = 3 ⋅ 1 = 3
For Box 3 ( second coin silver ):
N 3 = 3 ⋅ 2 = 6
For Box 4 ( second coin silver ):
N 4 = 3 ⋅ 3 = 9
Thus we have:
P ( Second Coin Silver ) = 4 8 0 + 3 + 6 + 9 = 8 3
Since we are not interested in the nature of the first coin chosen, it might as well not have been chosen - whether it is in our hand, or still in one of the boxes, does not matter. Thus we want the probability of picking a silver coin. All 1 6 coins are equally likely to be picked (there is an equal chance of picking each box, and an equal choice of choosing any coin in one box, so every coin has a chance of 4 1 × 4 1 of being chosen. Thus the probability of choosing a silver coin is 1 6 6 = 8 3 , making the anwer 1 1 .