Coin through a hole
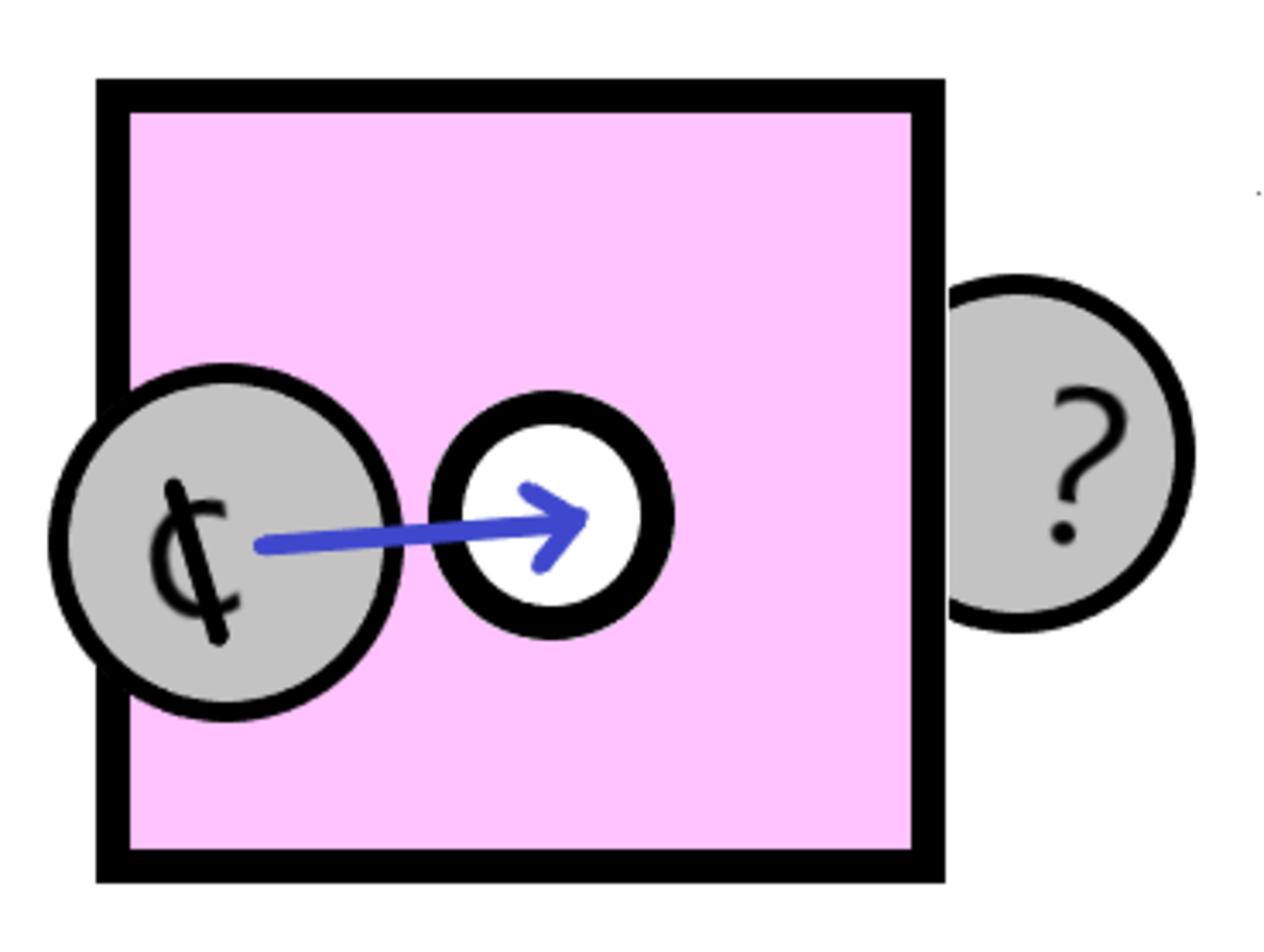
Take a piece of paper and cut out a perfect circle with diameter .
What is the diameter of the largest unaltered coin which may be passed through the hole without tearing it?
Pick the largest diameter that does not exceed the answer.
(Consider the coin to be very thin, and the paper to be very flexible and tear resistant, but not at all stretchy. You could also use a piece of film such as a plastic grocery bag.)
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The theoretical limit is π c m
If the paper is folded across the center of the hole, the hole becomes a half-circle that can be flattened out by pulling back the opposite sides of the crease. The hole then becoms a slit whose width is nearly half the circumference of the circle. The answer is then half the diameter of the hole minus the width of the coin.
3 c m gives enough room for a thin coin.