Coincidental decimal representation?
As shown by the calculators, the first 3 decimal places of 7 9 − 8 and 3 2 0 − 1 7 are both 0.888.
Which is larger?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
12 solutions
I admire your approach.
From the first line only it is immediate to see that D>0, because square root is concave.
Log in to reply
Hi Eric, could you elaborate further? How is that expressed using equations? Thanks.
how 80 square - 1 = 1-1 over 6400
Log in to reply
8 0 2 − 1 = 8 0 2 ( 1 − 8 0 2 1 ) = 8 0 2 ( 1 − 6 4 0 0 1 ) . The square root of this is 8 0 1 − 6 4 0 0 1 .
Starting with:
7 9 − 8 > < = 3 2 0 − 1 7
We can simplify to:
7 9 − 8 > < = 3 2 0 − 9 − 8
7 9 > < = 3 2 0 − 9
7 9 > < = 3 2 0 − 8 1
7 9 > < = 2 8 0 − 8 1
Generalizing to n:
n − 1 > < = 2 n − n + 1
n − 1 + n + 1 > < = 2 n
( n − 1 + n + 1 ) 2 > < = ( 2 n ) 2
n − 1 + 2 ( n − 1 n + 1 ) + n + 1 > < = 4 n
2 n + 2 ( n − 1 n + 1 ) > < = 4 n
n + n − 1 n + 1 > < = 2 n
n − 1 n + 1 > < = n
( n − 1 ) ( n + 1 ) > < = n
( n − 1 ) ( n + 1 ) > < = n 2
n 2 − 1 > < = n 2
Therefore the sign of the inequality is < for all positive real numbers and:
n − 1 < 2 n − n + 1
Moderator note:
The "><=" is also sometimes rendered as simply an equals sign with a question mark.
The use of any form of this symbol is somewhat controversial. (I personally have never seen it in an English textbook, only in French.) It's technically fine to use as long as each step is reversible and any changes in inequality direction are accounted for. For example, if both sides are multiplied by a negative at some single step, then the direction of inequality at the end would not be the same as at the start.
Great job on generalizing this
Why don't you write $\le$ instead of $<=$?
Log in to reply
I think he started intended to identify which inequality sign to use.
A better way is to simply start with an assumption, then prove later at the end. If the inequality proves false, then simply swap it accounting for =
In his last step for example, if we had generalized to n^2 - 1 > n^2 it's easy enough to prove that this is false, and the true inequality is n^2 - 1 < n^2
I also have never seen the ><= sign used, since it's just as easy to start with an assumption in most cases.
Merci beaucoup Thanks a lot
This solution is perfect!
Let , D Let, f ( x ) f ′ ( x ) x + 1 ⟹ f ′ ( x ) f ( x ) ⟹ 8 0 or ( 8 0 ⟹ D Thus, Alternate D Rationalizing D D ⟹ ⟹ D Thus, = ( 3 2 0 − 1 7 ) − ( 7 9 − 8 ) = 2 8 0 − 7 9 − 9 = ( 8 0 − 7 9 ) + ( 8 0 − 8 1 ) = x + 1 − x = 2 1 ( x + 1 1 − x 1 ) > x for positive reals < 0 for all x ≥ 0 is strictly decreasing − 7 9 > 8 1 − 8 0 − 7 9 ) + ( 8 0 − 8 1 ) > 0 > 0 ( 3 2 0 − 1 7 ) > ( 7 9 − 8 ) solution: = ( 8 0 − 7 9 ) + ( 8 0 − 8 1 ) the numerator, we get = ( 8 0 − 7 9 ) ( 8 0 + 7 9 ) ( 8 0 + 7 9 ) − ( 8 1 − 8 0 ) ( 8 0 + 8 1 ) ( 8 0 + 8 1 ) = ( 8 0 + 7 9 ) 1 − ( 8 0 + 8 1 ) 1 ( 8 0 + 7 9 ) < ( 8 0 + 8 1 ) ( 8 0 + 7 9 ) 1 > ( 8 0 + 8 1 ) 1 > 0 ( 3 2 0 − 1 7 ) > ( 7 9 − 8 )
Nice standard approach!
D = ( 8 0 − 7 9 ) + ( 8 0 − 8 1 )
It would be simpler from here if you just rationalized the numerators.
Log in to reply
Thanks!!!, i did not think about that . I will change the solution. :)
Log in to reply
Haha, no worries. Your solution works just fine too!
On the other had, can you explain why 8 0 − 7 9 is larger than 8 1 − 8 0 using second derivative?
This is a very creative method! Who knew trapezoidal rule works here?
How did you come up with this approach? Are there any other "approximating integrals technique" that are applicable as well? Like say midpoint rule, Simpson rule, quadrature rules, etc?
I need to copy this down. This is just superb. Thanks man!
Log in to reply
Thanks. The first step is similar to other solutions. The midpoint idea came from thinking about a geometrical interpretation of 2 sqrt(80) and then I realized the other term is the trapezoid area. I don't think Simpson's rule gives a definitive rule for over/underestimates if we only know the function is concave down. Btw, because we know the exact integral is 2/3 * (81) ^ 3/2 - 2/3 * (79) ^ (3/2), we also obtain: sqrt(320)-17 > 469-158/3*sqrt(79) > sqrt(79)-8.
Log in to reply
Oh this is a nice follow up question. You should post this tougher question too!
I worked out the repeating continued fraction expansions of both numbers: 3 2 0 − 1 7 = 1 + 7 + 1 + 3 4 + ⋱ 1 1 1 1 The sequence 1 , 7 , 1 , 3 4 repeats. The other number, 7 9 − 8 had 1 , 7 , 1 , 1 6 repeating. One may deduce the answer from that.
Postscript in response to comments: I DID NOT use the decimal expansion to find the continued fraction expansion. Since we know 1 7 2 < 3 2 0 < 1 8 2 , you have 3 2 0 − 1 7 = something > 1 1 , and then you say 3 2 0 − 1 7 = 3 2 0 + 1 7 3 2 0 − 1 7 2 = 3 2 0 + 1 7 3 1 (this is rationalizing the numerator) and that is equal to ( 3 1 3 2 0 + 1 7 ) 1 . Next, we have 3 2 0 + 1 7 between 3 4 and 3 5 , so dividing it by 3 1 we get something between 1 and 2 , so we have 1 + 3 1 3 2 0 − 1 4 1 . Now rationalize the numerator again, getting 1 + 3 2 0 + 1 4 4 1 . Keep going like that until you see the same expression you saw at an earlier step, and then you know it has to repeat.
Interesting approach, Michael! Could you explain how you found out the continued fractions?
Forgive me if I'm wrong, but isn't your solution circular? That is, you want to prove that one number is larger than the other, but you started with "these numbers can be represented in terms of its continued fractions", but in order to figure out the continued fraction form, we need to figure out the decimal representation of these 2 numbers first right? Or are you saying that it's possible to circumvent this step?
Log in to reply
I did not use the decimal expansion to find the continued fraction. I just iteratively rationalized the numerator. The decimal expansion does not tell you what the repeating part of the continued fraction is, but my method does.
Log in to reply
Ah got it got it. Thanks for the clarification. I learned something new today. Yay!
Relevant wiki: Jensen's Inequality
 Consider the function
f
(
x
)
=
8
1
−
x
−
(
9
−
2
1
x
)
.
Clearly,
f
(
0
)
=
0
. Now
f
′
′
(
x
)
=
4
(
8
1
−
x
)
3
/
2
−
1
<
0
,
showing that the function is convex on the interval
0
≤
x
≤
2
. Jensen's inequality states that
f
(
2
1
(
0
+
2
)
)
≥
2
1
(
f
(
0
)
+
f
(
2
)
)
,
i.e.
2
f
(
1
)
≥
f
(
2
)
.
Therefore
2
(
8
0
−
8
2
1
)
≥
7
9
−
8
,
that is,
3
2
0
−
1
7
≥
7
9
−
8
.
Consider the function
f
(
x
)
=
8
1
−
x
−
(
9
−
2
1
x
)
.
Clearly,
f
(
0
)
=
0
. Now
f
′
′
(
x
)
=
4
(
8
1
−
x
)
3
/
2
−
1
<
0
,
showing that the function is convex on the interval
0
≤
x
≤
2
. Jensen's inequality states that
f
(
2
1
(
0
+
2
)
)
≥
2
1
(
f
(
0
)
+
f
(
2
)
)
,
i.e.
2
f
(
1
)
≥
f
(
2
)
.
Therefore
2
(
8
0
−
8
2
1
)
≥
7
9
−
8
,
that is,
3
2
0
−
1
7
≥
7
9
−
8
.
How did you come up with the formula in the first place?
Which one?
The function f I defined because I recognized a pattern: we were asked to compare 2 ( 8 0 − 8 2 1 ) and 7 9 − 8 , which I quickly recognized as 2 ( 8 1 − 1 − ( 9 − 2 1 ⋅ 1 ) ) and 8 1 − 2 − ( 9 − 2 1 ⋅ 2 ) ; moreover, it was nice to see that 8 1 − 0 − ( 9 − 0 ) = 0 .
The Jensen inequality I used is generally true; for functions that are convex on an interval [ a , b ] , f ( s a + t b ) ≥ s ⋅ f ( a ) + t ⋅ f ( b ) with s + t = 1 ; s , t ≥ 0 . In this case, I chose [ a , b ] = [ 0 , 2 ] and s = t = 2 1 .
Log in to reply
Oh I didn't receive notification for this...
I like how you can motivate Jensen's out of a simple "which number is bigger?" question. I would have never thought about this. Thanks for teaching me something new, Mr Arjen.
There are plenty of wonderful solutions here, and I must say, yours is easily my favorite.
Log in to reply
I surprised myself with this, too :)
When I started solving the problem, I first sketched the functions 8 1 − x and 9 − 2 1 x , and focused on the vertical separation between the graphs. How could I prove that between x = 1 and x = 2 this vertical separation less than doubled ? Obviously this had something to do with the convexity of the square-root function. Then I remembered that Jensen formalized the connection between inequalities and convexity; from there it was not difficult to make the context "fit" into Jensen.
People are really bringing out the big guns for this problem. This can be done with simple algebra.
Generally, when comparing the numbers a + b and c + d , remember that addition and subtraction preserve order, as does squaring (as long as both sides of the inequality are positive). The simple thing to do is rearrange terms so the integers are on one side of the inequality while the radicals are on the other side. Then square. Sort terms one more time, square again, and look at the final inequality.
In this case 7 9 − 8 < 3 2 0 − 1 7 ⇔
9 < 3 2 0 − 7 9 ⇔
8 1 < 3 9 9 − 2 ∗ 3 2 0 ∗ 7 9 ⇔
2 ∗ 3 2 0 ∗ 7 9 < 3 1 8 ⇔
4 ∗ 3 2 0 ∗ 7 9 < 3 1 8 ∗ 3 1 8 ⇔
1 0 1 1 2 0 < 1 0 1 1 2 4 Since the last inequality is true, the first one is also true.
simplest solution
The answer is ✓(320)-17
Here's how I rationalize this WITHOUT using a calculator. ...
If:
✓(320)=2×✓(80)
&
-17= 2×(-8.5)
And we also know that:
✓(80) > ✓(79)
and:
-8 > -8.5
Then it would stand to reason that:
2×✓(80) > ✓(79)
&
-8 > 2(-8.5)
Which also means that:
2×[✓(80)-8.5] > ✓(79)-8
And because :
2×[✓(80)-8.5]= ✓(320)-17
We can conclude that:
✓(320)-17> ✓(79)-8
Therefore the answer is:
✓(320)-17
And:
✓(80) > ✓(79)
&
8.5. > 8
Then it would stand to reason that:
2×[✓(80)-8.5] > ✓(79)-8
Just because a > b and c > d are true, how do you know that 2 ( a − c ) > b − d must be true as well?
Log in to reply
I corrected the solution...Also, I am sorry that I misspelled your name. It was not intentional :-(
@Pi Han Gig
I meant to say
-17=2×(-8.5)
and -8 > -8.5
----Below is the corrected statement----
The answer is ✓(320)-17
Here's how I rationalize this WITHOUT using a calculator. ...
If:
✓(320)=2×✓(80)
&
-17= 2×(-8.5)
And:
✓(80) > ✓(79)
and:
-8 > -8.5
Then it would stand to reason that:
2×✓(80) > ✓(79)
&
-8 > 2(-8.5)
Which means that:
2×[✓(80)-8.5] > ✓(79)-8
And because :
2×[✓(80)-8.5]= ✓(320)-17
We can conclude that:
✓(320)-17> ✓(79)-8
Therefore the answer is:
✓(320)-17
* My apologies
Square both expressions so that the difference increases ☺
Find a^2 -b^2 by multiplying by the conjugate. Compare 320-289 with 79-64 31 > 15
So you end up comparing the values of 1 4 3 − 1 6 7 9 and 6 0 9 − 2 7 2 5 . How are you supposed to know which of these numbers is larger?
We will first conjecture that sqrt(320) - 17 > sqrt(79) - 8 and set out to apply inequality algebra to prove were right.
1) Add +17 to both sides: sqrt(320) > sqrt(79) + 9.
2) Square both sides: 320 > 79 + 18
sqrt(79) + 81,
320 > 160 + 18
sqrt(79)
160 > 18 * sqrt(79)
3) Square to check:
25,600 > (18^2) * 79
25,600 > 324 * 79
25,600 > 25,596. check.
Henceforth, sqrt(320) - 17 > sqrt(79) - 8. QED.
These numbers 7 9 and 3 2 0 are not perfect squares. The roots of the previous perfect square are subtracted from the root of each number. the root. So, both the two expression will obviously yield 0 point something. The further away they are from the previous perfect square, the greater their roots. Since 3 2 0 − 1 7 2 = 3 1 is greater than 7 9 − 8 2 = 1 5 , the answer is the latter option.
No, this is incorrect. By your logic, 2 5 7 − 1 6 = 1 0 2 5 − 3 2 .
Log in to reply
How? I didn't say anything of that sort.
Log in to reply
257 and 320 are not perfect squares.
Since you said:
The further away they are from the previous perfect square, the greater their roots.
And because the "distance between these radicals and their greatest integer value are the same, then the greater their roots."
It never occurred to me to do it /without/ a calculator...
Yes, we can obviously get the answer without using a calculator, but the fun part lies on "how do we solve this problem without a calculator?"
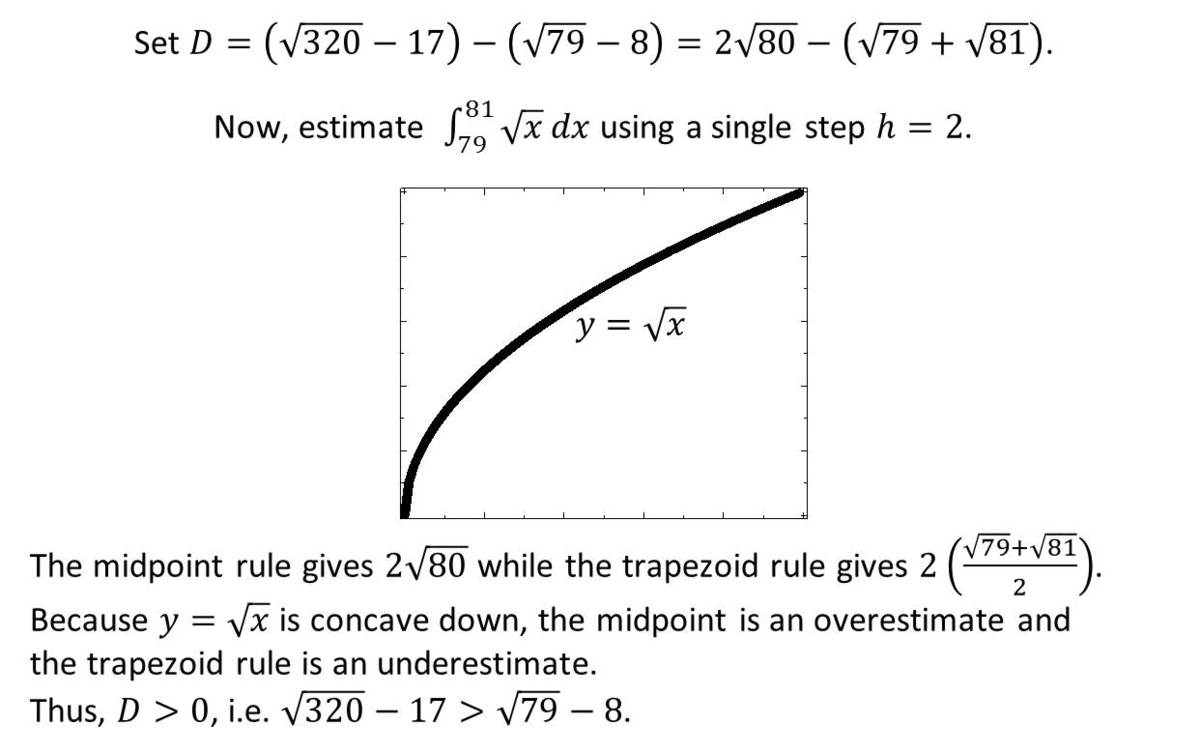
We have that D = ( 3 2 0 − 1 7 ) − ( 7 9 − 8 ) = 2 8 0 − 7 9 − 9 = 2 8 0 − ( 7 9 + 8 1 ) .
Now ( 7 9 + 8 1 ) 2 = 7 9 + 8 1 + 2 7 9 × 8 1 = 1 6 0 + 2 ( 8 0 − 1 ) ( 8 0 + 1 ) =
1 6 0 + 2 8 0 2 − 1 = 1 6 0 + 1 6 0 1 − 6 4 0 0 1 < 1 6 0 + 1 6 0 = 3 2 0 .
Thus 7 9 + 8 1 < 3 2 0 = 2 8 0 , and so D > 0 , i.e., 3 2 0 − 1 7 > 7 9 − 8 .