Collect Gold Coins in LatticeVille

The important thing to consider is there is a limited number of North and East steps that you can take. Whatever path Benjie and Esther take, they can only go 4 steps to the North and 7 steps to the East . So the total number of steps each of them can take will always be $4+7=11$ .

You can consider this problem as an arrangement of N's and E's. They can have multiple paths, but the number of N's and E's will remain the same, whatever the arrangement.

Relevant wiki: Rectangular Grid Walk

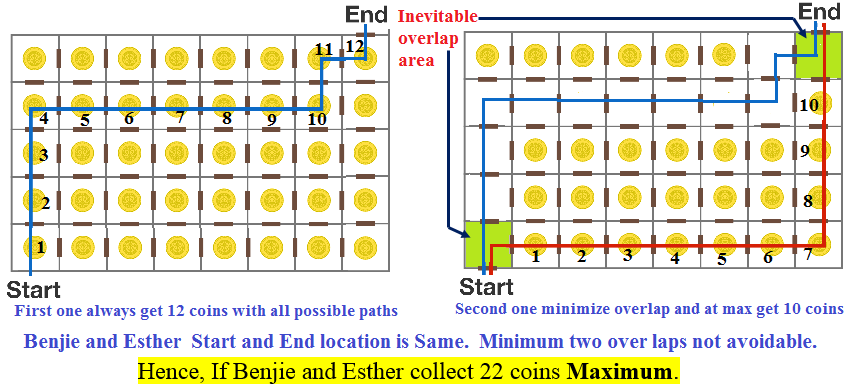No, more than 22 coins is not possible. From the possible rout options one can collect 12 coins from the start location to the end location. Benjie & Esther can collect maximum of 12 + (12 - 2) =22 coins, where the minimum overlap of 2 coins in start and end location is subtracted in the above calculation since it is already taken by Benjie.

Note : Explorers are only able to move North and/or East through the rooms. Hence the number of moves in North & East will be same with all possible roots.

Think of the grid on your maths squares when you studied vectors.

Let: Start Point to furthest Right Corner = Vector B

Let: Furthest Right Corner to End Point = Vector C

Vector B + Vector C = Vector A

No matter what way you travel you will always be adding up to Vector A

Or to go from the corner of Flinders & Spencer to Carlton Gardens you would use always use the same energy using the same rules (assuming no stopping at lights or short cuts!)

Oh, Agnishom Chattopadhyay and your LatticeVille problems.

The answer is, of course, no, since in order to move from the start to the finish they must take 4 steps up and 7 steps right, meaning if they don't cross paths, they can collect 12 coins each. However, since the start and end intersect their paths, they only collect 22 coins as a maximum. They don't intersect in this set of paths, making it one of 5250 possible optimal solutions.

It's easy to see that one person can collect at most 12 coins. Since start and end rooms are same for both people, the other person can collect 12 - 2 = 10 coins max. Therefore it isn't possible to collect more than 12 + 10 = 22 coins.

Suppose B was exploring the rooms by himself. Every time he goes through a door (except for the last one at the NE corner) he will find a coin. He goes through five doors when moving north, and seven doors when moving east, and so by himself B can collect 12 coins, no matter what path he takes from entrance to exit. He cannot collect more than 12.

Similarly, exploring by herself E could collect 12 coins. She cannot collect more than 12.

So can E and B together collect 12+12 =24 coins? NO! because both of them must visit the first room at the lower left corner, and the last room at the upper right corner, and only one of them can collect a coin from those rooms. So at most they can collect 24-2=22 coins when working together.

Can this maximum be achieved? YES! In many ways - in particular by taking the paths provided by the proposer!

This is a standard problem adopted from Manhattan Distance.