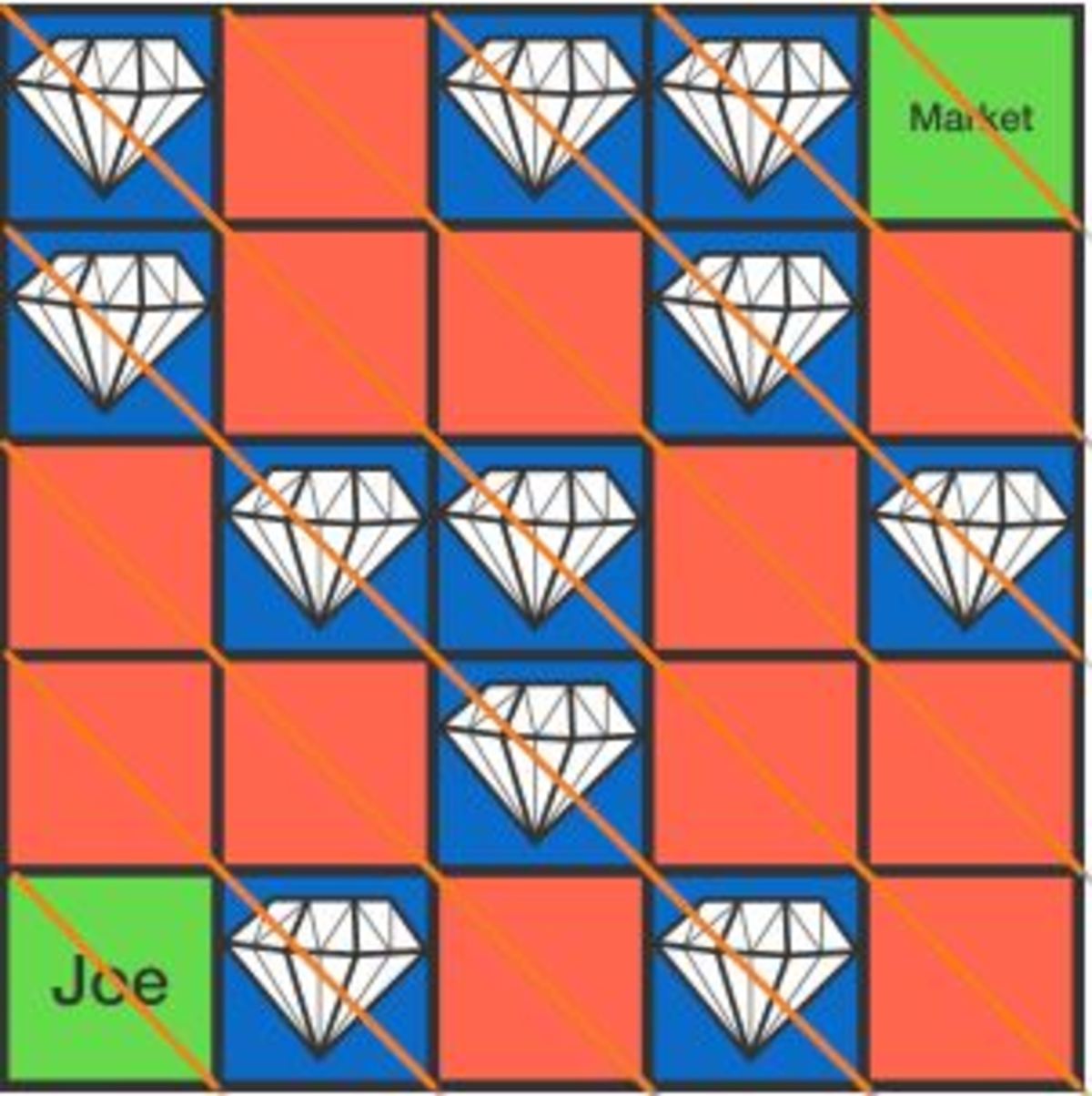
Collecting Gems

No matter which of the 70 possible paths Joe chooses, he must pass through 7 boxes with a gem or a guard. If there are $x$ guards, then he will be left with $y = \text{gems} - \text{guards} = (7-x) - x = 7 - 2x$ gems when he reaches the market. To maximize $y$ we must minimize $x$ .

The minimum number of guards on a path is $x = 2$ : go two steps to the right, then all the way to the top, then all the way to the right. This leaves $y = 7 - 2\cdot 2 = \boxed{3}$ gems to the market.

Quick check: nowhere along this path does Joe run out of gems...

And here we let the computer sort it out:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

final int WIDTH = 5, HEIGHT = 5;
int map[][] =
    {   { 0, 1, -1, 1, -1 },
        { -1, -1, 1, -1, -1 }, 
        { -1, 1, 1, -1, 1}, 
        { 1, -1, -1, 1, -1 },
        { 1, -1, 1, 1, 0 }
    };    
int score[][] = new int[WIDTH][HEIGHT];

score[0][0] = 0;
for (int s = 1; s < WIDTH+HEIGHT-1; s++)
    for (int x = 0; x <= s; x++) {
        int y = s - x; if (x < WIDTH && y < HEIGHT) {
            int sc1 = (x > 0) ? score[x-1][y] : -1;
            int sc2 = (y > 0) ? score[x][y-1] : -1;

            int sc = (sc1 < 0 || sc2 > sc1) ? sc2 : sc1;

            score[x][y] = (sc < 0) ? -1 : sc + map[x][y];
        }
    }

System.out.println(score[WIDTH-1][HEIGHT-1]);

Each position of the map is assigned a value map[x][y] representing the gain or loss for passing that point: $-1$ for a guard, $+1$ for a gem.

We keep track of the number of gems Joe is carrying in an array score[x][y] , starting with score[0][0] = 0 at the starting point. Now we move upward in diagonals, i.e. $x + y = s$ for $s = 1, 2, \dots$ . Thus we first consider $(0,1)$ and $(1,0)$ ; then $(0,2), (1,1), (2,0)$ ; and so on, until we read the destination score[WIDTH][HEIGHT] . This will end up containing the answer to the problem.

For each point on the grid $(x,y)$ , we look at its neighbors to the left and down: $(x-1,y)$ and $(x,y-1)$ . We choose the highest of both (to optimize the number of gems). A negative value indicates that the neighbor lies of the grid, or that Joe has insufficient gems to make it through; in other words, score[x][y] < 0 means "inaccessible". Finally, we add to the highest score of accessible neighbors the gain or loss of the new box; this is the highest number of gems with which the box can be reached, and this we store in score[x][y] .

The output of this program is 3 , in agreement with the analysis above.

We went firstUp up right up up right right then we reach market this is the easiest way.

Index the $25$ squares as $(i,j)$ with $(1,1)$ in the lower left and $(5,5)$ in the upper right. The only legal moves are $(i,j) \rightarrow (i,j+1)$ and $(i,j) \uparrow (i+1,j)$ .
For $n = 2$ to $10$ let the set $S_n = \{(i,j) | i+j = n\}$ . It's clear every path goes from $S_2$ to $S_3$ to ... to $S_{10}$ . None of the intermediate seven sets can be avoided. Now note that both $S_4$ and $S_7$ contain only guards and no diamonds. Thus any path must hit at least two guards and at most five diamonds. Thus the maximum possible return is $3$ diamonds. This can be achieved by taking the path $(1,1) \rightarrow (1,2) \rightarrow (1,3) \uparrow (2,3) \uparrow (3,3) \uparrow (4,3) \uparrow (5,3) \rightarrow (5,4) \rightarrow (5,5).$

This problem can be solved using Bellman-Ford Algorithm which algorithm search the minimum in this case maximum value of a vertex if there are negative weights, here the implementation in C++:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54

#include <bits/stdc++.h>

#define X 5
#define Y 5

using namespace std;

typedef pair<int,int> ii;
typedef vector<ii> vii;

int dx[] = {1,0};
int dy[] = {0,1};

vii listvertex;

int main(){

int mapweight[5][5] = {{0,1,-1,1,-1},
                       {-1,-1,1,-1,-1}, 
                       {-1,1,1,-1,1}, 
                       {1,-1,-1,1,-1},
                       {1,-1,1,1,0}};

int value[X][Y];

for(int x = 0; x < X; x++)
for(int y = 0; y < Y; y++)
{
value[x][y] = 0;
listvertex.push_back(make_pair(x,y));
}

for(auto u = listvertex.begin(); u < listvertex.end(); u++)
for(int i = 0; i < 2; i++){

ii w_static = *u;
ii w = w_static;

if( (w.first + dx[i] < X) && (w.second + dy[i] < Y) &&
    (w.first + dx[i] >= 0) && (w.second + dy[i] >= 0) ){

w.first += dx[i]; w.second += dy[i];

if(value[w_static.first][w_static.second] + mapweight[w.first][w.second] >= 0){
value[w.first][w.second] = max(value[w.first][w.second],
               value[w_static.first][w_static.second] + mapweight[w.first][w.second]);
}
}

}

cout<<"Maximum Gems: "<<value[X-1][Y-1]<<endl;

}

The total number of steps for any given path is 8 steps. If we minimize the amount of red squares we step on, we will maximize the amount of gems he has.

We can see that finding a one red square solution is impossible after trying things. Next, we try a two step solution, and we find one. (It's right-right-up-up-up-up-right-right)

Counting the number of gems we get in this solution, we find that we have 3 gems left.

Assuming all the red blocks are gaurding and all the blue blocks are gems the shortest route would be go to the middle of the bottom row, the way up the middle column and finally all the way right with 3 gems.

I noticed that Joe will visit 7 places on his way to the market, because of the limitation on his movement (up/right). Each place he visits lies on a diagonal of potential visits per step (see screenshot below). Step 1's diagonal allows two different places to be visited, step 2 has 3 different places, etc.

Notice that step 2 & 5 have no diamonds, hence in theory the maximum diamonds Joe will be able to get is 1-1+1+1-1+1+1 = 3

When checking for a possible path, I found: Right, Up, Right, Up, Right, Up, Up, Right.

There are many variations to this path. Key diamonds to get are the first diamond after stepping right, the diamond in the middle (as you can never reach the one in the top-left afterwards), and the one directly left to the market.

that is what I did. Also, what sort of jails have GEMS 💎 in them? Jail is a place for criminals and one of the most common crimes is stealing so I am not surprised 😳 on why the criminals haven't stolen them yet? Plus, if the jail guard takes so many gems just because someone needs to visit the market or toilet, they must be really, REALLY rich by now.