[College Calc 01-02. Limits of Sequences] #08
Suppose we are cutting a flat, circular disk n times in a straight line. Let L n denote the maximum number of pieces it can yield. Given
n → ∞ lim ( L n − p n ) = q
for some reals p , q , find p + q .
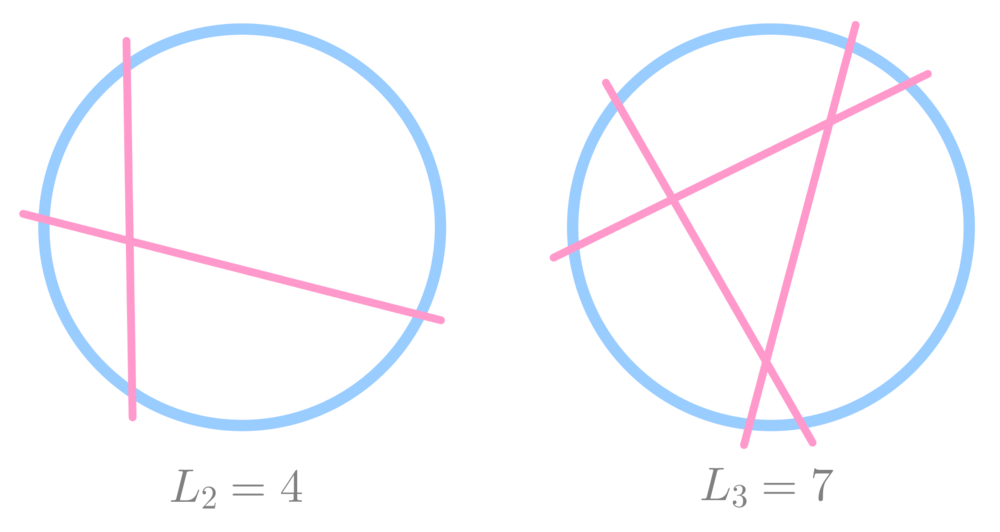 An example of when
n
=
2
,
3
An example of when
n
=
2
,
3
This is a part of the College Calc problem set. You can find more problems here .
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
i did the same but reported wrong answer
We note that L 0 = 1 , L 1 = 2 , L 2 = 4 , L 3 = 7 , ... The terms are related as follows:
L k + 1 k = 0 ∑ n L k + 1 L n + 1 + k = 0 ∑ n L k − L 0 L n + 1 ⟹ L n = L k + k + 1 = k = 0 ∑ n L k + k = 0 ∑ n k + k = 0 ∑ n 1 = k = 0 ∑ n L k + 2 n ( n + 1 ) + n + 1 = 2 n ( n + 1 ) + n + 2 = 2 ( n − 1 ) n + n + 1 = 2 n 2 + n + 2 For k ≥ 0 Note that L 0 = 1 Replace n + 1 with n .
Then we have:
q = n → ∞ lim ( L n − p n ) = n → ∞ lim ( 2 n 2 + n + 2 − p n ) = n → ∞ lim 2 n 2 + n + 2 + p n 2 n 2 + n + 2 − p 2 n 2 = n → ∞ lim 2 n 2 + n + 2 + 2 n 2 n 2 + n + 2 − 2 n 2 = n → ∞ lim 2 n 2 + n + 2 + 2 n 2 n + 2 = n → ∞ lim 2 1 + 2 n 1 + n 2 1 + 2 1 2 1 + n 1 = 2 2 1 Multiply up and down by 2 n 2 + n + 2 + p n For the limit q to exist, p = 2 1 . Divide up and down by n .
Therefore p + q = 2 1 + 2 2 1 = 2 2 3 = 4 3 2 .
This sequence has its own name: The Lazy Caterer's Sequence .
Suppose we have cut the disk 2 times, yielding L 2 = 4 pieces, and we want to make another cut so that the number of pieces is maximal. When a cut passes through a piece, the piece is split into two, effectively increasing the number of pieces by 1 , as illustrated below.
That means, we want to maximize the number of pieces the cut passes through. But can a cut pass through every piece? No. When a cut "moves on" to another piece, it has to pass a line. (Otherwise the piece would be the same one as the previous one.) Note that, however, a cut can only meet at most once with each of the other cuts. In this case, there are two lines present, so that the additional cut may pass through at most 3 pieces, such that L 3 ≤ L 2 + 3 = 7 . More generally, L n + 1 ≤ L n + n + 1 .
However for us to say that L n + 1 = L n + n + 1 , we must also prove that such a cut -- meeting with all of the previous cuts inside the circle -- is attainable. Trying to prove that in a fixed circle is difficult, but we can prove it in a different way by thinking in reverse.
Imagine we have made n cuts such that the number of pieces is maximized. We note that increasing the size of the circle, with its center fixed, will not influence the number of pieces. (If it increased the number of pieces, then that would be a contradiction, because the cuts are supposed to be maximal.) We can easily draw a line, not parallel to any of them, and also avoiding their intersections. This way, the line has met all of the n lines. Now we increase the size of the circle, with its center fixed, such that all of the intersections are in its interior. Then, we indeed have a cut that meets with all of the previous n cuts inside the circle.
We now have the recurrence relation
L n + 1 = L n + n + 1 ,
such that adding these n − 1 equations --
L 2 L 3 L 4 ⋮ L n = L 1 = L 2 = L 3 = L n − 1 + 2 + 3 + 4 + n
-- would yield
L n = L 1 + k = 2 ∑ n k = 2 + 2 n ( n + 1 ) − 1 = 2 1 n 2 + 2 1 n + 1 .
Then, finding the limit is not too difficult. In order for
n → ∞ lim ( L n − p n )
to converge, we must have p = 2 1 = 2 2 . Referring to the solution of this problem we easily find that
n → ∞ lim ( 2 1 n 2 + 2 1 n + 1 − 2 1 n 2 ) = 2 2 1 2 1 = 4 2 .
Thus, p + q = 2 2 + 4 2 = 4 3 2 .