[College Calc 01-02. Limits of Sequences] #09
Suppose a particle is bouncing orthogonally between two parallel surfaces A and B.
A scientist has noticed a trend: after each additional bounce of the particle, the average speed of the particle during the last two trips between the surfaces halves down.
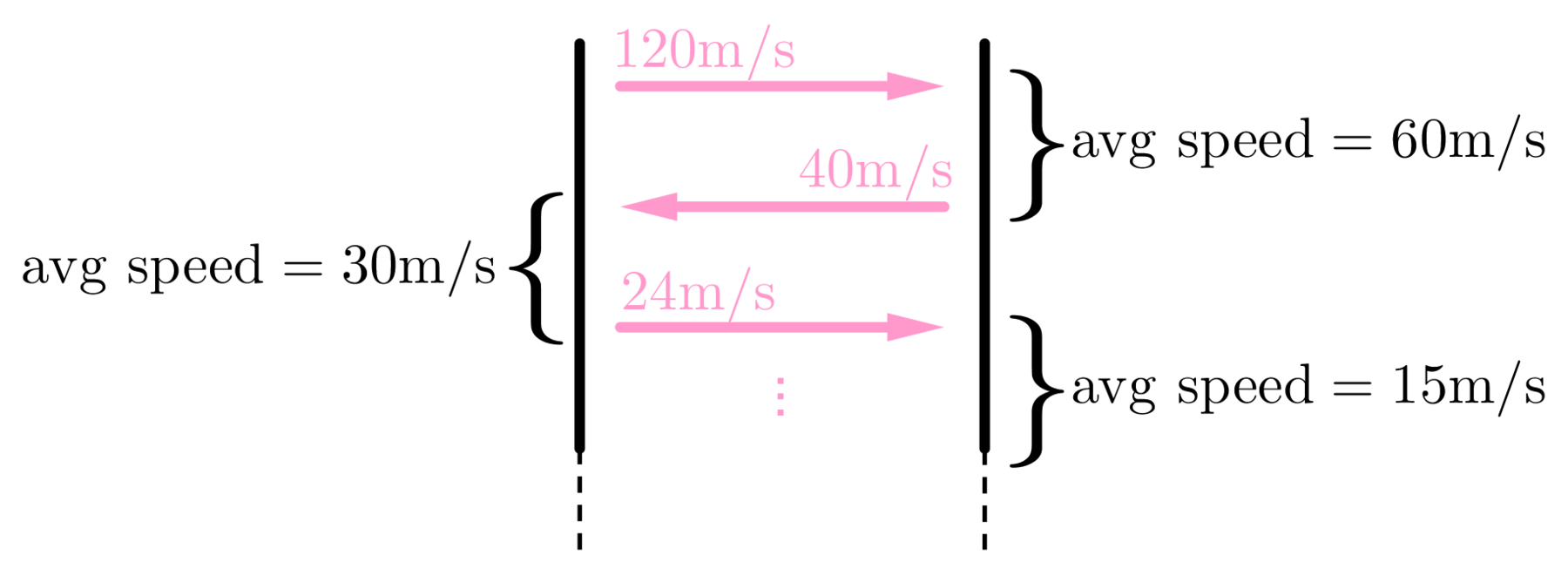 An illustrative diagram of the relation between two consecutive trips
An illustrative diagram of the relation between two consecutive trips
Let a n m / s be the average speed of one trip. Given a 1 = 1 2 0 and a 2 = 4 0 , find
n → ∞ lim 4 n ∣ a n − 2 a n + 1 ∣ .
Assumptions:
-
The particle only moves orthogonally to the surfaces, its direction unchanged unless it bounces off the surface.
-
The particle touches the surface before bouncing off immediately.
-
Any quantum mechanical phenomena are disregarded, i.e. approach the problem purely mathematically.
This is a part of the College Calc problem set. You can find more problems here .
The answer is 135.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
If the distance between the surfaces is s and the average speed from trip n − 1 and trip n is v n , then we have: v n = t n − 1 + t n 2 s = a n − 1 s + a n s 2 s = a n − 1 + a n 2 a n − 1 a n ( 1 ) We are given that 2 v n + 1 = v n . Substituting ( 1 ) in this equation we get: a n + a n + 1 4 a n a n + 1 = a n − 1 + a n 2 a n − 1 a n a n − 1 ( a n + a n + 1 ) = 2 a n + 1 ( a n − 1 + a n ) a n + 1 = 2 a n + a n − 1 a n a n − 1 Upon dividing both the numerator and the denominator by a n a n − 1 and taking the reciprocal, we get: a n + 1 1 = a n 1 + a n − 1 2 For simplicity we denote b n = a n 1 and the above equation is rewritten in: b n + 1 = b n + 2 b n − 1 ⇔ b n + 2 = b n + 1 + 2 b n ( 2 ) b 1 = a 1 1 = 1 2 0 1 b 2 = a 2 1 = 4 0 1 This looks very similar to the Fibonacci sequence. We'll derive b ( n ) in a way, similar to how Binet's formula for Fibonacci numbers is derived. First, suppose b n is a geometric progression with a quotient k . We can make this supposition, because calculating the first 10-15 elements of b n we notice that the quotient b n b n + 1 converges. In other words as n → ∞ b n turns in a geometric progression. So let's use b n = b 1 k n − 1 and substitute this in ( 2 ) : b 1 k n + 1 = b 1 k n + 2 b 1 k n − 1 ∣ : b 1 k n − 1 = 0 k 2 − k − 2 = 0 This quadratic has 2 solutions: k = 2 ; k = − 1 , which explains why b n isn't really a geometric progression. Now we write b n = A . 2 n + B ( − 1 ) n . To find the values of the coefficients A and B we'll use what we found for b 1 and b 2 : { b 1 = A . 2 + B ( − 1 ) = 1 2 0 1 b 2 = A . 2 2 + B ( − 1 ) 2 = 4 0 1 From this system we find A = 1 8 0 1 , B = 3 6 0 1 and so: b n = 1 8 0 2 n + 3 6 0 ( − 1 ) n = 3 6 0 2 . 2 n + ( − 1 ) n = 3 6 0 2 n + 1 + ( − 1 ) n ⇒ a n = b n 1 = 2 n + 1 + ( − 1 ) n 3 6 0 Let X = a n − 2 a n + 1 . X = 2 n + 1 + ( − 1 ) n 3 6 0 − 2 n + 2 + ( − 1 ) ( − 1 ) n 7 2 0 X = ( 2 . 2 n + ( − 1 ) n ) ( 4 . 2 n − ( − 1 ) n ) 3 6 0 ( 2 n + 2 − ( − 1 ) n − 2 . 2 n + 1 − 2 ( − 1 ) n ) X = 2 n . 2 n ( 2 + ( − 2 1 ) n ) ( 4 − ( − 2 1 ) n ) 3 6 0 ( 2 n + 2 − 2 n + 2 − 3 ( − 1 ) n ) X = 4 n ( 2 + ( − 2 1 ) n ) ( 4 − ( − 2 1 ) n ) − 1 0 8 0 ( − 1 ) n Taking the absolute value of the expression above results in the removal of all minus signs in the numerator and transforming ( − 1 ) n into 1 or: ∣ X ∣ = 4 n ( 2 + ( − 2 1 ) n ) ( 4 − ( − 2 1 ) n ) 1 0 8 0 x → ∞ lim 4 n ∣ X ∣ = x → ∞ lim 4 n ( 2 + ( − 2 1 ) n ) ( 4 − ( − 2 1 ) n ) 4 n 1 0 8 0 = ( 2 + 0 ) ( 4 − 0 ) 1 0 8 0 = 1 3 5 In the limit we used that for ∣ x ∣ < 1 lim n → ∞ x n = 0 .
Set our time unit such that the first traversal takes one unit of time. We get t 1 = 1 , t 2 = 3 , t 3 = 5 etc.
The halving velocity criterion can be expressed as a double time criterion: t n + 1 + t n = 2 ( t n + t n − 1 )
From this we get t n + 1 = 2 t n − 1 + t n
It it easy to show that t n = 2 t n − 1 + 1 ⇒ t n + 1 = 2 t n − 1 and similarly t n = 2 t n − 1 − 1 ⇒ t n + 1 = 2 t n + 1
From the initial values and the recurrence relations, we conclude that t n are the Jacobsthal numbers : t n − 1 = J n = 3 2 n − ( − 1 ) n
We can now rewrite the expression
a n − 2 a n + 1 = 1 2 0 ( 2 n + 1 − ( − 1 ) n + 1 3 − 2 2 n + 2 − ( − 1 ) n + 2 3 ) = 3 6 0 ( 2 n + 1 − ( − 1 ) n + 1 ) ( 2 n + 2 − ( − 1 ) n + 2 ) 2 n + 2 − ( − 1 ) n + 2 − 2 ( 2 n + 1 − ( − 1 ) n + 1 ) = 3 6 0 ( 2 2 n + 3 − 2 n + 2 ( − 1 ) n + 1 ) − ( − 1 ) n + 2 2 n + 1 + ( − 1 ) 2 n + 3 3 ( − 1 ) n + 1
In the limit, only the highest order powers remain, so n → ∞ lim 4 n ∣ a n − 2 a n + 1 ∣ = n → ∞ lim 2 2 n × 3 6 0 × 2 2 n + 3 3 = 3 6 0 × 8 3 = 1 3 5
Let d be the distance between the surfaces; the time it takes for the particle to travel back and forth with average speed a n and a n + 1 respectively is
t = a n d + a n + 1 d .
Then, the average speed of the particle is
t 2 d = a n d + a n + 1 d 2 d = a n 1 + a n + 1 1 2 ;
the harmonic mean of a n and a n + 1 .
Note that the average speed during the first two travels equals 1 2 0 1 + 4 0 1 2 = 6 0 ( m / s ) . Since this needs to half down every time n increases by 1 , we may write this as
a n 1 + a n + 1 1 2 = 6 0 ⋅ ( 2 1 ) n − 1 ,
or simply,
a n 1 + a n + 1 1 = 6 0 2 n ⋯ E q 1 ( n ) .
Let us now write b n = a n 1 for readability. Note that subtracting E q 1 ( n − 2 ) from E q 1 ( n − 1 ) yields
b n − b n − 2 = 6 0 2 n − 1 − 2 n − 2 = 6 0 2 n − 2 ⋯ E q 2 ( n )
For n = 2 k , adding the equations E q 2 ( 4 ) , E q 2 ( 6 ) , ⋯ , E q 2 ( n ) yields
b 2 k = b 2 + 6 0 2 2 3 4 k − 1 − 1 = 3 6 0 2 2 k + 1 + 1 .
Similarly, we have
b 2 k − 1 = b 1 + 6 0 2 1 3 4 k − 1 − 1 = 3 6 0 2 2 k − 1 .
In general,
b n = 3 6 0 2 n + 1 + ( − 1 ) n .
(This can also be proved by finding some appropriate a such that c n + c n + 1 = ( b n + a ⋅ 2 n ) + ( b n + 1 + a ⋅ 2 n + 1 ) = 0 ; such a solution is left as an exercise for the readers.)
Now for the desired limit, we first evaluate
a n − 2 a n + 1 = 2 n + 1 + ( − 1 ) n 3 6 0 − 2 n + 2 + ( − 1 ) n + 1 7 2 0 = 3 6 0 ⋅ ( 2 n + 1 + ( − 1 ) n ) ( 2 n + 2 + ( − 1 ) n + 1 ) ( − 1 ) n + 1 − 2 ( − 1 ) n = ( 2 n + 1 + ( − 1 ) n ) ( 2 n + 2 + ( − 1 ) n + 1 ) − 1 0 8 0 ( − 1 ) n .
Then, we may easily have
n → ∞ lim 4 n ∣ a n − 2 a n + 1 ∣ = n → ∞ lim 4 n ∣ ∣ ∣ ∣ ( 2 n + 1 + ( − 1 ) n ) ( 2 n + 2 + ( − 1 ) n + 1 ) − 1 0 8 0 ( − 1 ) n ∣ ∣ ∣ ∣ = n → ∞ lim 4 n 2 2 n + 3 1 0 8 0 = 1 3 5 .