[College Calc 01-02. Limits of Sequences] #05
Let a n be a sequence of real numbers inductively defined by
a 1 = 3 ; a n + 1 = 4 1 a n 2 + 2 1 a n − 2 .
Given that n → ∞ lim a n exists, find its value.
This is a part of the College Calc problem set. You can find more problems here .
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Let the limit (provided it exists) be l
Then l = 2 l 2 − 4 ⟹ l = 4 , − 2
Since a n < 0 for n ≥ 3 , therefore the required limit is − 2 .
But it doesn't converge. Nor is it true that " a n < 0 for n ≥ 3 ".
The first few values are
| n | a n |
| 1 | 3 |
| 2 | 0 . 5 |
| 3 | − 3 . 8 7 5 |
| 4 | 3 . 5 0 7 8 1 2 5 |
| 5 | 2 . 1 5 2 3 7 4 … |
| 6 | − 1 . 6 8 3 6 4 2 … |
Thanks. This problem was previously flawed and has been rectified.
In the future, if you have concerns about a problem's wording/clarity/etc., you can report the problem. See how here .
Obviously the sequence may not converge at all, but the question asks if it converges, what would be the limit? Let the limit be λ ; then
λ 2 λ λ 2 − 2 λ − 8 ( λ − 4 ) ( λ + 2 ) = 2 1 λ 2 − 4 = λ 2 − 8 = 0 = 0
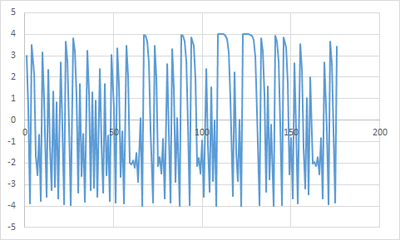
So if the limit exists, it can either be 4 or − 2 . But the actual values of a n are always less than 4 (I don't know how to prove this). The graph show the first values of a n . Hence the limit is − 2 .
Thanks. This problem was previously flawed and has been rectified.
In the future, if you have concerns about a problem's wording/clarity/etc., you can report the problem. See how here .
It really doesn't make sense to ask "what would be the limit if it did converge?" when the sequence doesn't actually converge. You discard 4 as a possibility because the sequence never reaches 4 ; but it doesn't reach − 2 either.
Anyway, because the original question actually has a closed form solution (which I found really surprising), I've included that with my solution of the updated problem. You'll be able to see from that why ∣ a n ∣ can't be greater than 4 , and why it won't reach either of the fixed points.
Since we've had two problems for the price of one here, here are two solution methods for this kind of question.
The first idea is to treat this as an iterated function system.
Let f ( x ) = 4 1 x 2 + 2 1 x − 2 .
The fixed points of this function are found by solving x = f ( x ) ; that is x = 4 1 x 2 + 2 1 x − 2
There are two fixed points; x = 4 and x = − 2 . The important thing to consider is their stability. We have
f ′ ( x ) = 2 1 x + 2 1
so f ′ ( 4 ) = 2 5 and f ′ ( − 2 ) = − 2 1 .
A fixed point x is only stable if ∣ f ′ ( x ) ∣ ≤ 1 ; hence x = 4 is unstable and x = − 2 is stable, and, in the limit, the iteration will tend to x = − 2 for all starting points except x = 4 and one other value (left as a bonus question, if you've read this far; all that matters here is that it's not 3 ).
Hence the required limit is − 2 .
The original recurrence was a 1 = 3 ; a n + 1 = 2 1 a n 2 − 4
As observed elsewhere, this sequence doesn't converge; but it doesn't go off to infinity, or enter a cyclic pattern either.
Again, there are two fixed points, but using the method above, neither of them is stable.
The first few values are
and it doesn't really settle down after that.
Dividing both sides of the recurrence by 4 , we find
( 4 a n + 1 ) = 2 ( 4 a n ) 2 − 1
This form should look familiar; it's similar to the identity cos 2 θ ≡ 2 cos 2 θ − 1
With this in mind, then, put a n = 4 cos x n
We then have the very simple recurrence x n + 1 = 2 x n
When n = 1 , 4 cos x 1 = 3 ; so the full solution is a n = 4 cos ( 2 n − 1 cos − 1 4 3 )
Although we proved above that 4 and − 2 are not stable fixed points, it's another nice exercise to show from this trig form that a n can't reach these values.