Collide and break!

Classical Mechanics Level 2

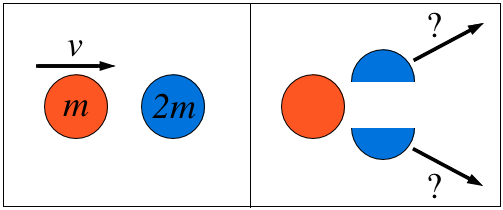
A body of mass $m$ is moving along the $x$ -axis with speed $v$ when it collides with a body of mass $2m$ initially at rest. After the collision, the first body comes to rest and the second body splits into two pieces of equal mass that move with equal velocities at equal angles off the $x$ -axis $0 < \theta < 90^\circ$ , as shown in the figure.

Which of the following statements correctly describes the speeds of the two pieces?

Each piece moves with speed v. Each piece moves with speed less than v/2. Each piece moves with speed v/2. Each piece moves with speed greater than v/2.

1 solution

Sahil Bansal
Jan 21, 2016

Let's conserve momentum along the $x$ -axis. Before the collision, the total momentum in the horizontal direction is $mv.$ After the collision, the horizontal velocity of each piece is given by $mv'\cos \theta,$ where $v'$ is the velocity we're interested in. (Note, the lower piece makes an angle of $-\theta$ , but $\cos \theta = \cos(-\theta).$ )

As there are two such pieces, the total momentum is then $2mv'\cos \theta$ which must be equal to $mv$ by conservation:

$mv = 2mv'\cos \theta \longrightarrow \frac{v}{2\cos \theta} = v'$

Since $\cos \theta$ is never bigger than or equal to 1, it must be that the left hand side is larger than $\frac{v}{2}$ .

You can also add that the speed must be less than v as this would otherwise violate energy conservation, and also momentum conservation for some angles of theta.

Andrew Normand - 4 years, 4 months ago

Collide and break!

1 solution

0 pending reports