Colliding Spheres

Classical Mechanics Level 1

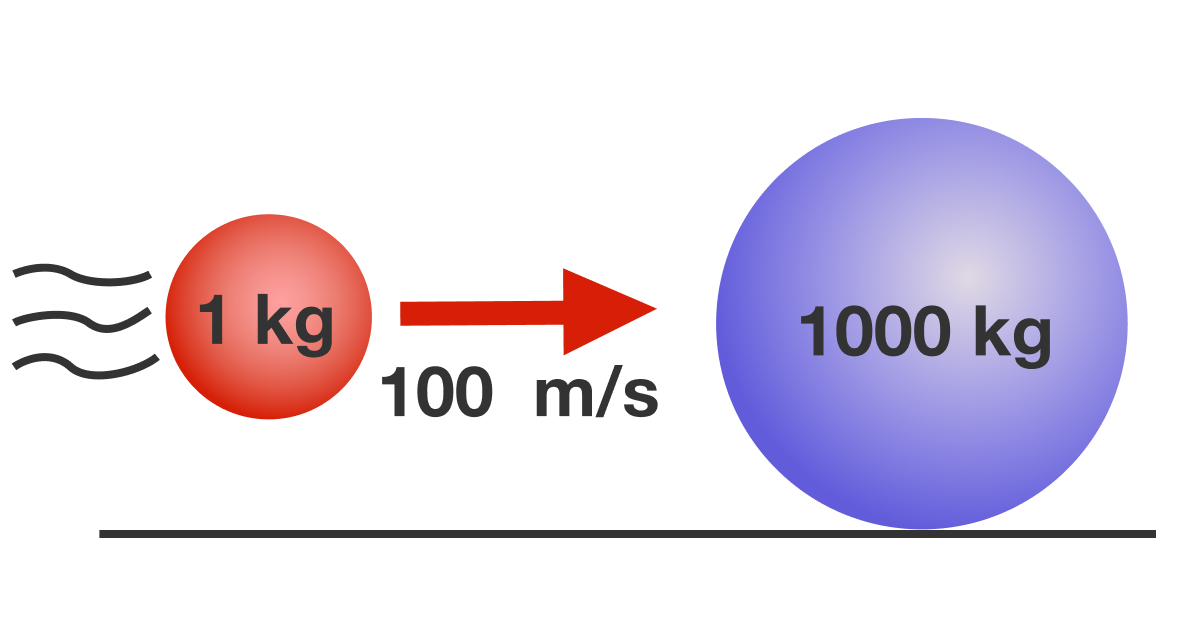
A sphere of mass 1 kg is traveling with velocity 100 m/s toward a stationary sphere of mass 1000 kg. The two spheres collide elastically. What is the total kinetic energy (in Joules) of the spheres after the collision?

Assume that both spheres have the same radius. All surfaces are smooth. There is no rolling motion.

The answer is 5000.

1 solution

Pranshu Gaba
Jan 19, 2016

Recall that kinetic energy is conserved during an elastic collision. Therefore the total kinetic energy of the system by collision is equal to the total kinetic energy of the system after the collision.

The total kinetic energy of the system is:

$\text{ KE} = \sum \frac{ 1 } {2 } m_{i} v_{i}^{2 } = \frac{ 1 } {2} \times 1 \times 100^{2} + \frac{ 1 } { 2 } \times 1000 \times 0 ^{2} = \boxed{ 5000 \text{ J}} ~~~~ _\square$

Correct me if I am wrong. We have the first scenario: 1x100^2/2 = 5000, But if we use P1=P2 -> M1xV1=M2xV2 we find that V2= 100x1/1001 =0.09

If we calculate the kinect energy with the information of the second scenario we find KE=m.v^2/2 -> 1001x(0.09)^2/2 = 4.9

In elastic collisions no kineck energy is lost, same for momentum, but why I found a different value for KE ?

José Vinícius - 5 years, 3 months ago

From the look of it, you combined the two masses as M2. You actually treated the problem as a totally inelastic collision. For this problem, you will instead have to use M1xV1 = M1xV1' + M2xV2' in addition to the conservation of kinetic energy to find the velocities.

Luke Yoon - 5 years, 3 months ago

Let use this P like u use it in your demonstration... Let say P1 as the entity before collision and P2 after collision... So before collision P1 = m1.v1 and after collision P2 = m1.v1' + m2.v2 but we have conservation of Energy so Energy before and after are conserved... P1 = P2. V2 = 0 because m2 is motionless So m1.v1 = m1.v1' +m2.v2 ----> m1.v1 = m1.v1' + m2x0 ----> m1.v1 = m1.v1' ----> v1 = v1' Velocity remained the same. In your demonstration, what make u wrong is you combined both mass as a single mass ... In elastic collision masses are not combined as a single object instead they separate after collision.

Roger Djedje - 5 years, 3 months ago

Assuming no rotation occurs E = 1/2 mv^2 = 5000 (conserved in elastic collision.) which is the right answer.

Alas, there IS a rotation. The writer of the problem wrote "..rolls toward " which means the rotational energy is unaccounted for. The problem is compounded as the rotation is not specified.. Hence the problem is ill-stated.

Therefore, the correct answer is not an equality E=5000 but inequality E >= 5000

Agustinus Law - 5 years, 3 months ago

Thanks. I have edited the problem accordingly.

Pranshu Gaba - 5 years, 3 months ago

got it .good solution. upvoted

Satyabrata Dash - 5 years, 3 months ago

Colliding Spheres

The answer is 5000.

1 solution

0 pending reports