Collinear Intersections
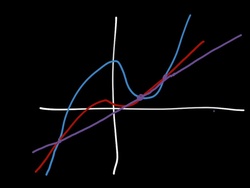 The graph of
y
=
2
x
3
−
4
x
+
2
intersects with the graph of
y
=
x
3
+
2
x
−
1
at three collinear points. Find the slope of the collinear points.
The graph of
y
=
2
x
3
−
4
x
+
2
intersects with the graph of
y
=
x
3
+
2
x
−
1
at three collinear points. Find the slope of the collinear points.
The answer is 8.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Fantastic solution! Commendable idea.
Crsly cool solution!!! Thnx!!!
F o r p o i n t o f i n t e r s e c t i o n x , a n d y v a l u e s w i l l b e t h e s a m e . ⟹ 2 x 3 − 4 x + 2 = x 3 + 2 x − 1 . ∴ x 3 − 6 x + 3 = 0 . s o l v i n g c u b i c , x = − 2 . 6 6 9 1 , . 5 2 4 0 , 2 . 1 4 5 1 . U s i n g y = x 3 + 2 x − 1 , w e g e t . x − 2 . 6 6 9 1 = − 2 5 . 3 5 3 1 , x 2 . 1 4 5 1 = 1 3 . 1 6 0 8 . S l o p e = ( 2 . 1 4 5 1 − ( − 2 . 6 6 9 1 ) 1 3 . 1 6 0 8 − ( − 2 5 . 3 5 3 1 ) = 8 . 0 0 0 0 6 .
Subtracting the equation of the first line from the equation of the other, we get:
x 3 − 6 x + 3 = 0 = f ( x )
The polynomial must have three real roots due to three intersections. Let the roots be named a , b , c .
Hence, f ( a ) = f ( b ) = f ( c ) = 0
Consider the polynomial g ( x ) = x 3 + 2 x − 1
g ( x ) = ( x 3 − 6 x + 3 ) + ( 8 x − 4 )
g ( x ) = f ( x ) + ( 8 x − 4 )
Hence, g ( a ) = f ( a ) + ( 8 a − 4 )
Therefore, g ( a ) = 8 a − 4
Therefore, in a similar manner,
g ( a ) = 8 a − 4
g ( b ) = 8 b − 4
g ( c ) = 8 c − 4
Consider the intersection points. The graph intersects at a , b , c . So we need to find the slope by picking two out of three of them. This time we will choose a and b .
Slope = Δ x Δ y = b − a g ( b ) − g ( a ) = b − a ( 8 b − 4 ) − ( 8 a − 4 ) = b − a 8 ( b − a ) = 8