Collision and the phase space

Classical Mechanics Level 2

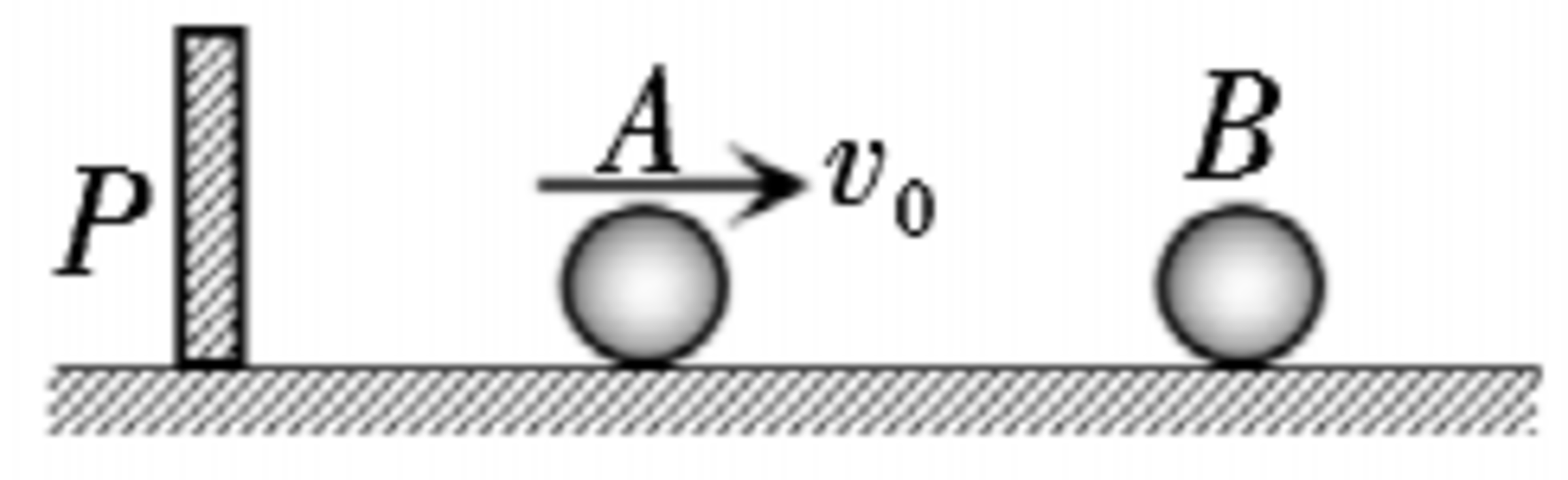
As shown above, on a frictionless plane, the ball A A whose mass is m m is moving at the velocity v 0 v_0 and collides with the ball B B whose mass is 4 m 4m and velocity is 0 0 .

After the collision, A A moves backwards with the velocity ∣ v ∣ = α v 0 |v|=\alpha v_0 where 0 < α < 1 0<\alpha<1 and has elastic collision with a fixed board P P .

If A A can eventually catch up and collide with B B , how many of the followings would be a appropriate value of α \alpha ?

A. 1 2 \dfrac{1}{2}

B. 2 5 \dfrac{2}{5}

C. 2 3 \dfrac{2}{3}

D. 1 7 \dfrac{1}{7}

4 1 2 3

Alice Smith by Alice Smith , 20, China

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Linear momentum conservation equation in the case of first collision between the balls is m v 0 = 4 m v − m α v 0 mv_0=4mv-mαv_0 or v = α + 1 4 v 0 v=\dfrac{α+1}{4}v_0 . Therefore the condition of the problem requires α > α + 1 4 α>\dfrac{α+1}{4} or α > 1 3 α>\dfrac{1}{3} . The two options 2 5 \dfrac{2}{5} and 2 3 \dfrac{2}{3} meet the requirement.

1 Helpful 0 Interesting 0 Brilliant 0 Confused

What about α = 1 2 \alpha = \dfrac{1}{2} ?

Hosam Hajjir - 1 year, 8 months ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...