Collision Course On The Plaza
Three cats are standing at the corners of Equilateral Triangle Plaza. At a time , the cats turn towards their feline counterpart to their left, and begin running towards said cat at a constant speed of m/s. If Equilateral Triangle Plaza has a side length of metres, then how much time after , in seconds , will the cats take to collide in the centroid of the plaza?
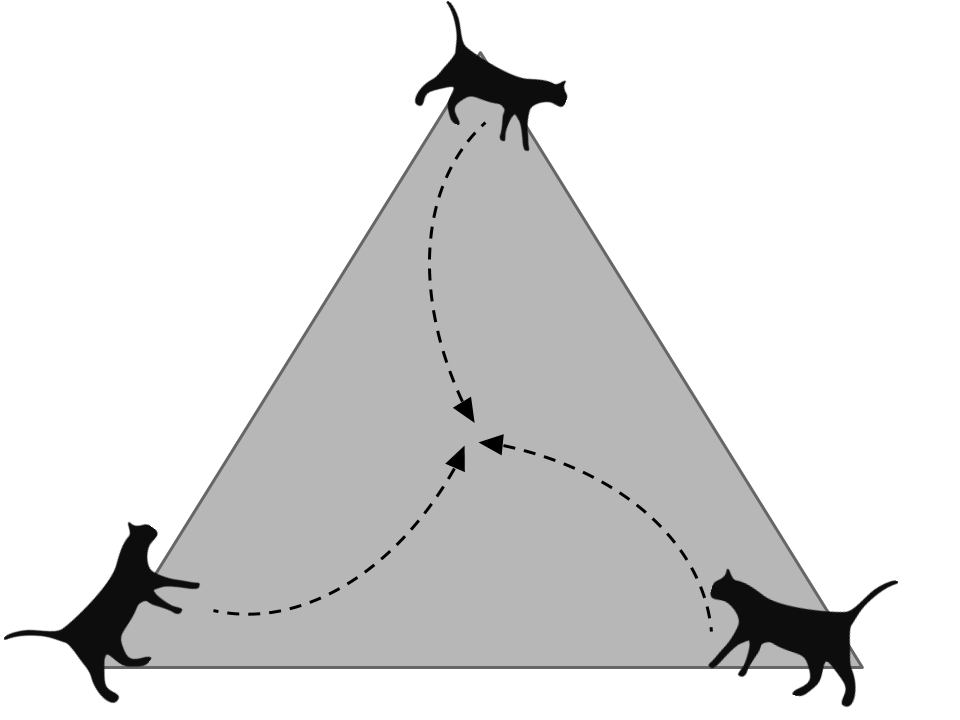
Neglect all random variables. (i.e. the cats' initial acceleration, as well as friction, variations in 'plaza' topography, drag, etc.)
The answer is 18.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The key is to exploit the symmetry within the problem. In fact, if we take a snapshot of the three cats at any time t 1 between T 0 and T 0 + Δ t , they will be forming an equilateral triangle relative to each other, which shrinks and counterclockwise as t 1 approaches T 0 + Δ t . We can then draw this diagram:
Cat B 's velocity vector can be separated into two component vectors, one of magnitude 5 3 m/s pointing perpendicular from Cat A 's velocity vector, and one of magnitude 5 m/s pointing 'towards' Cat A 's velocity vector. As Cat A 's velocity vector has a magnitude of 1 0 m/s, the combined effect is as if Cat A were running towards Cat B at a velocity of 1 5 m/s. The question asks for Δ t : as Cat A has velocity 1 5 m/s, the cats will collide in 1 5 2 7 0 = 1 8 seconds.
Note that it was okay to calculate the time for only Cat A , as all three cats collide at the same time.