Collision in Spring Mass System!
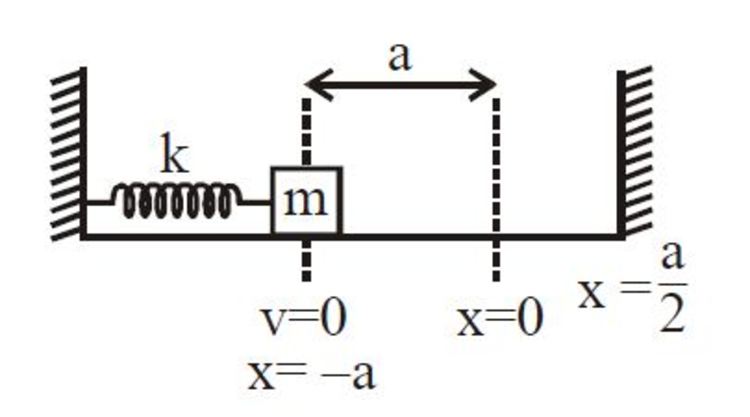 A spring (spring constant
k
) having one end attached to rigid wall & other end attached to a block of mass
m
kept on a smooth surface as shown in figure. Initially spring is in its natural length at
x
=
0
, now spring is compressed to
x
=
−
a
and released. (Coefficient of restitution
e
=
2
1
). If velocity of block just after first collision is
a
1
6
m
n
k
. Find the value of
n
.
A spring (spring constant
k
) having one end attached to rigid wall & other end attached to a block of mass
m
kept on a smooth surface as shown in figure. Initially spring is in its natural length at
x
=
0
, now spring is compressed to
x
=
−
a
and released. (Coefficient of restitution
e
=
2
1
). If velocity of block just after first collision is
a
1
6
m
n
k
. Find the value of
n
.
The answer is 3.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
I'm astonished to see this problem at level 4. This is not even level 3 man!!
P.E. converted to K . E . = 2 1 ∗ k { a 2 − ( 2 a ) 2 } = 2 1 ∗ k { 4 3 ∗ a 2 } K . E . g a i n e d = 2 1 ∗ m ∗ V 2 . ⟹ V = a m k ∗ 4 3 . B u t v e l o c i t y A F T E R c o l l i s i o n = 2 1 ∗ V = 2 1 ∗ a m k ∗ 4 3 = a 4 1 ∗ m k ∗ 4 3 = a 1 6 m 3 ∗ k = a 1 6 m n ∗ k . n = 3
The coefficient of restitution is defined as the ratio of the speed after to the speed before a collision. So, in this case, the answer is half of the speed before the collision (which we can find from conservation of energy).
0 . 5 k ( a 2 − ( 0 . 5 a ) 2 ) = 0 . 5 m V i 2 ⇒ V i = a 4 m 3 k
V f = 0 . 5 V i = a 1 6 m 3 k ⇒ n = 3
We neglect the effect of the spring during the collision by letting the duration of the collision go to zero.