Collision inbound
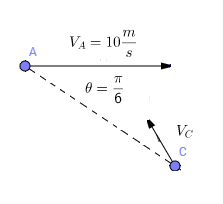
Two particles, and move in the same plane with constant velocities. The magnitude of velocity of is . The velocity vector of initially makes an angle of 30 degrees with the line joining and . What must be the minimum magnitude of velocity of in S.I units, such that they collide?
The answer is 5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
(Everything is expressed in SI unit, i have omitted writing units.)
Let initial distance between A and C be A C = k . This remains constant.
Now let velocity of C be x and let the time when they meet be t .
Assume that they meet at point H.
Thus, AH = 10t and CH = xt and AC=k
Applying cosine rule in triangle ACH,
cos 3 0 ∘ = 1 0 t k k 2 + 1 0 0 t 2 − ( x t ) 2
Arranging a little bit, t 2 ( 1 0 0 − x 2 ) − ( 1 0 3 k ) t + k 2 = 0
Now since t is real, the above equation's discriminant should be greater than or equal to 0.
⟹ 3 0 0 k 2 − 4 0 0 k 2 + 4 ( x k ) 2 ≥ 0
⟹ x ≥ 5