Collision + observation
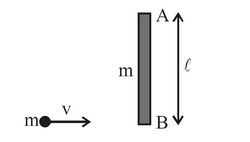 A particle of mass
strikes with a rod of mass
at its one of end as shown in diagram with
, without sticking to the rod. If we observe the rod and particle from the point
on the rod, then:
A particle of mass
strikes with a rod of mass
at its one of end as shown in diagram with
, without sticking to the rod. If we observe the rod and particle from the point
on the rod, then:
Angular momentum of rod and particle will be conserved just before and just after collision.
Linear momentum of rod and particle will be conserved.
Observed motion of rod after collision will be pure rotation.
Observed motion of particle will be straight line after collision.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.