Collision
Classical Mechanics
Level
3
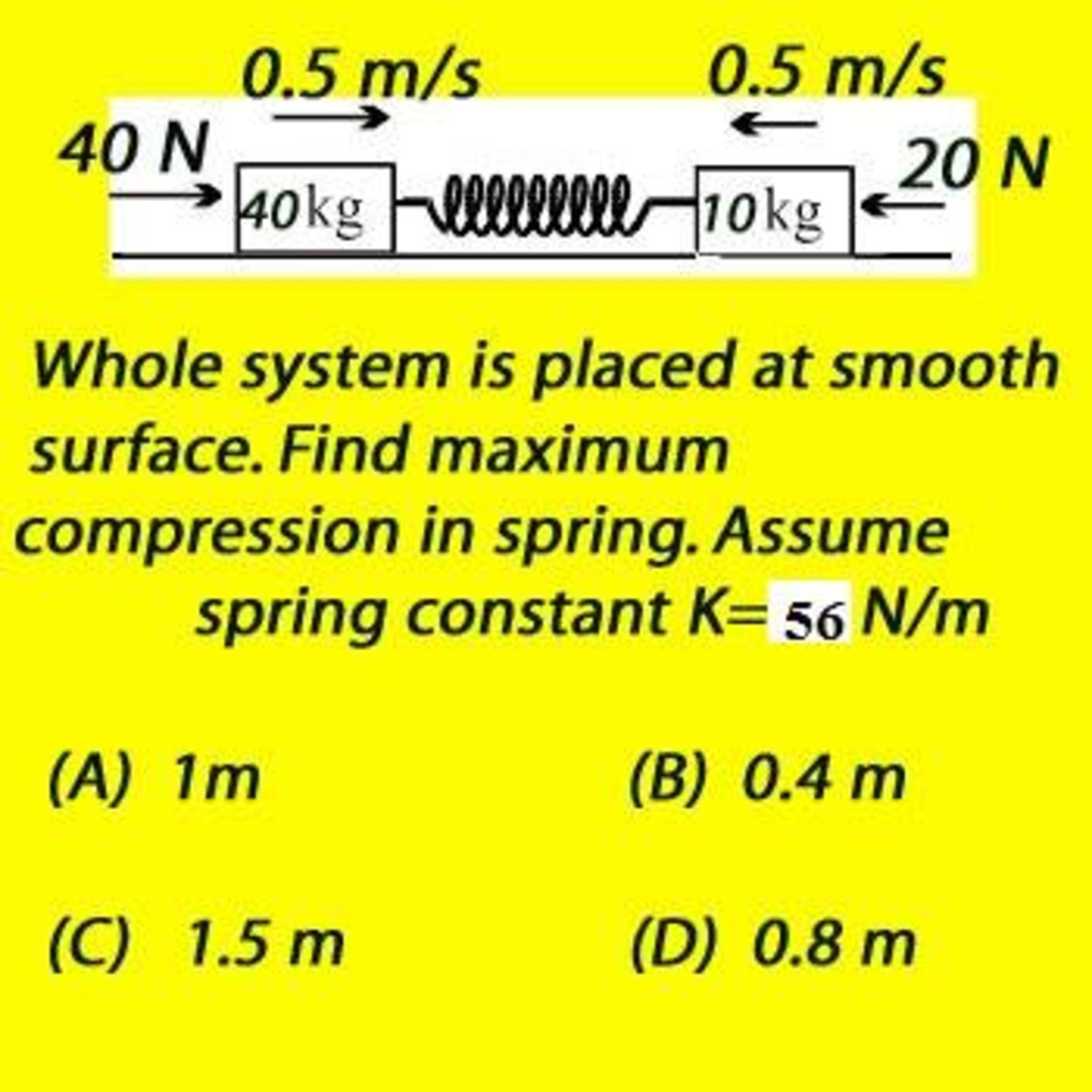
Whole system is placed at smooth surface, find the maximum compression of spring?
0.4m
1.5m
1m
0.8m
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The equation of relative motion of the two body system is :
d t d v r e l = m 2 F 2 − m 1 F 1 − μ F 1 2 . Here F 1 = 4 0 N is the force applied to the body of mass m 1 = 4 0 kg., F 2 = 2 0 N is the force applied to the body of mass m 2 = 1 0 kg., F 1 2 is the force exerted by the spring on the bodies, equal to 5 6 x r e l N, x r e l is the displacement of the first body relative to the second, v r e l is their relative velocity, and μ = m 1 + m 2 m 1 m 2 = 8 kg. is the reduced mass of the system. Solving this equation using the initial condition we get
v r e l 2 = 1 + 6 x r e l − 7 x r e l 2 .
When the spring compression is maximum, v r e l = 0 . This will happen when 7 x r e l 2 − 6 x r e l − 1 = 0 ⟹ x r e l = 1 m.