Color Travel
A regular tetrahedron is colored as shown, so that the ration of yellow to green areas is
. If every dot of color were to travel along a straight line through the center of the tetrahedron to the opposite surface, what would be the ration of yellow to green be then?
Details:
-
Every face is originally divided into four equal sized equilateral triangles, with the middle triangle yellow and the remaining ones green.
-
During the operation, all of the color drains from its original location.
-
If O is the center of the tetrahedron, then for every point A on its surface, the new location for the same color, A’, is at the intersection of line AO with the surface of the tetrahedron past O.
-
Find the ratio of total yellow area to total green area after the operation.
-
Put the ratio in the format , where and are coprime positive integers, and type in your answer as . For example if you believe the ratio to be , type in .
The answer is 3.1.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Every vertex has as it opposite a center of a face and vice versa. A center of an edge will project to the center of the opposite edge. And the opposite of a straight line will again be either a straight line (since a straight line and a point define a plane, which intersects another plane in a straight line) or a series of straight-line segments if on more than one face.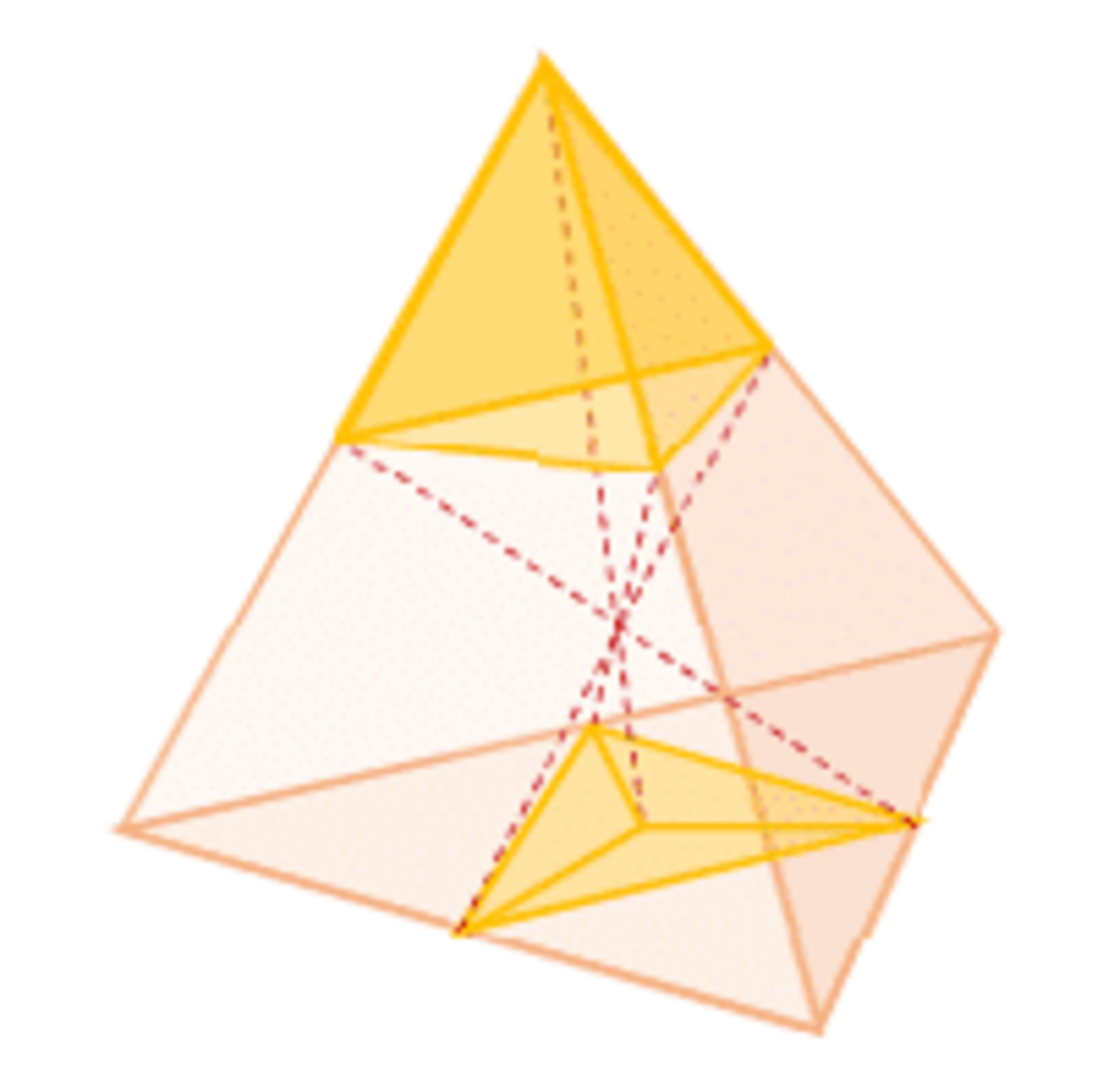
The yellow triangle on the bottom face will project onto three such triangles centered at the opposite vertex. (The image shows the portions of the original triangle going to each of the new ones.) Similarly the three green triangles around a vertex will project into just one triangle in the center of the opposite side. In effect the colors will switch places and the ratio of yellow to green will be 3 : 1 .