(Color+beauti)ful Hexagon!
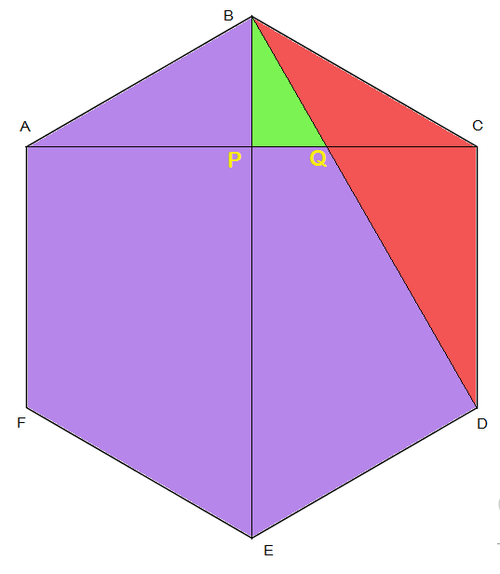 As shown in the above figure, in a
regular
hexagon
A
B
C
D
E
F
, the segments
B
D
,
B
E
,
C
A
are drawn.
As shown in the above figure, in a
regular
hexagon
A
B
C
D
E
F
, the segments
B
D
,
B
E
,
C
A
are drawn.
B D and C A intersect at point Q .
B E and C A intersect at point P .
A ( △ B P Q ) is colored green
A ( △ B C D ) is colored red
Rest of the area is colored purple
If the ratio of areas of colors
purple : green : red = a : b : c
such that a , b , c ∈ N , gcd ( a , b , c ) = 1 .
Find a + b + c
The answer is 36.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
I've edited the LaTeX of your solution, please see how to use LaTeX mathematical formatting , use it when you post problems and solutions, to make it appear just the way you see it in books :) @Subrata Dutta
First note that Δ B C D is congruent to Δ A B C . Now ∠ B C D = 1 2 0 ∘ , so as Δ B C D is isosceles we have that ∠ C B D = 3 0 ∘ , so ∠ P B Q = ∠ P B C − ∠ C B D = 3 0 ∘ .
The ratio of the areas of Δ P B Q to Δ P B C is then tan ( 6 0 ∘ ) tan ( 3 0 ∘ ) = 3 1 .
Then since the area of Δ P B C is 2 1 that of Δ A B C , and hence of Δ B C D as well, the ratio of the areas of the green triangle to the red triangle is 1 : 6 .
Next, let O be the center of the hexagon. Then ∠ B O D = ∠ B C D = 1 2 0 ∘ , and thus the red triangle is 2 1 the area of quadrilateral O B C D . But the area of O B C D is 3 1 that of the hexagon, and thus the area of the red triangle is 6 1 that of the hexagon.
So now suppose the area of the hexagon is 3 6 . The area of the red triangle would then be 6 , and hence the area of the green triangle 1 . This would then give us an area for the purple region of 3 6 − 6 − 1 = 2 9 . Thus the desired ratio of areas of colors purple:green:red is 2 9 : 1 : 6 , and so a + b + c = 2 9 + 1 + 6 = 3 6 .
ah.. its a problem difficult to look at but easy when we do it..
Δ
B
C
D
≡
Δ
A
B
C
.
.
.
.
(
1
)
∴
∠
C
B
D
(
i
.
e
.
∠
C
B
Q
)
=
∠
B
A
C
.
.
.
(
2
)
Let AB=BC=CD=DE=1.
I
n
Δ
A
B
C
,
A
B
=
B
C
,
∠
A
B
C
=
1
2
0
o
∴
∠
B
A
C
=
∠
A
C
B
=
3
0
o
=
∠
Q
B
C
b
y
(
2
)
∵
o
f
s
y
m
m
e
t
r
y
,
Δ
P
B
A
≡
Δ
P
B
C
.
∴
Δ
P
B
C
i
s
a
9
0
:
6
0
:
3
0
.
.
.
.
(
3
)
∠
P
B
C
=
6
0
o
.
.
.
.
.
(
4
)
∠
P
B
Q
=
∠
P
B
C
−
∠
Q
B
C
=
3
0
o
.
I
n
Δ
Q
B
P
,
∠
Q
P
B
=
9
0
o
,
∠
P
B
Q
=
3
0
o
∴
T
h
i
s
i
s
6
0
:
3
0
:
9
0
Δ
.
(
5
)
I
n
a
3
0
o
:
6
0
o
:
9
0
o
Δ
,
A
R
E
A
=
8
H
y
p
.
2
∗
3
=
6
(
B
i
g
l
e
g
)
2
∗
3
.
S
i
d
e
=
1
,
h
e
x
a
g
o
n
a
l
a
r
e
a
=
2
3
∗
3
.
.
.
.
.
.
(
6
)
F
r
o
m
(
5
)
a
r
e
a
Δ
P
B
Q
=
6
B
P
2
∗
3
=
6
(
2
1
)
2
∗
3
=
2
4
3
F
r
o
m
(
3
)
a
r
e
a
Δ
P
B
C
=
8
B
C
2
∗
3
=
8
3
=
2
a
r
e
a
Δ
A
B
C
=
2
a
r
e
a
Δ
B
C
D
.
.
.
f
r
o
m
(
1
)
.
∴
A
r
e
a
o
f
Δ
B
C
D
=
4
3
P
u
r
p
l
e
a
r
e
a
=
h
e
x
a
g
o
n
a
l
a
r
e
a
−
r
e
d
a
r
e
a
−
g
r
e
e
n
a
r
e
a
.
=
2
3
∗
3
−
4
3
−
2
4
3
.
{
2
3
∗
3
−
4
3
−
2
4
3
}
:
4
3
:
2
4
3
:
:
{
3
6
−
1
−
6
}
:
1
:
6
∴
{
3
6
−
1
−
6
}
+
1
+
6
=
3
6
Thank you, Mr. Brian, the equivalence of ABC and BCD,
was taken from your solution.
That avoided construction of Altitude in BCD.
If each side is a , then B P = 2 a , P Q = 2 3 a , A C = a 3 and A ( △ B C D ) = A ( △ A B C ) and now its easy.