${\color{#3D99F6} \mathbf{blue}}$ and ${\color{#D61F06} \mathbf{red}}$ Tiles

Probability Level 3

You have plenty of ${\color{#3D99F6} \mathbf{blue}}$ and ${\color{#D61F06} \mathbf{red}}$ $1 \times 2$ tiles (at least six of each):

How many ways can you use them to tile a $6 \times 2$ grid?

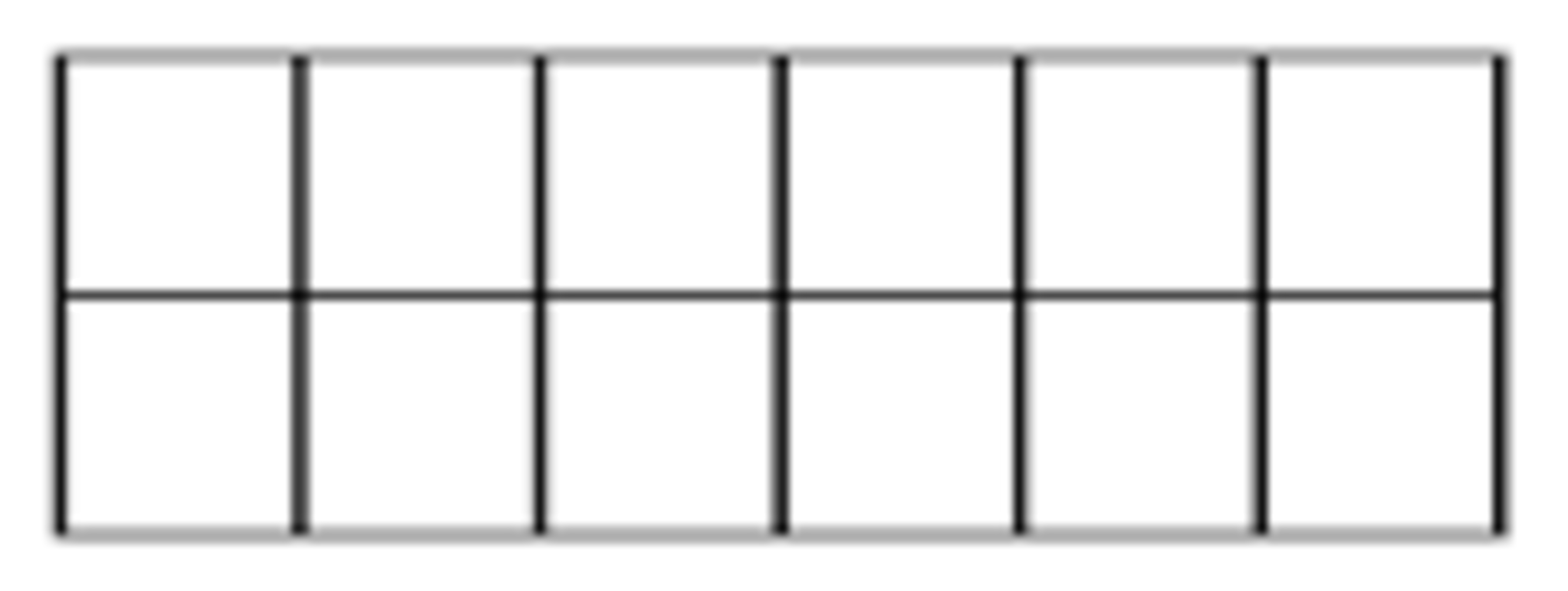
Assumptions :

The entire grid must be covered
No overlaps or tiles outside the boundary
The tiles can be oriented veritcally or horizontally

The answer is 832.

1 solution

Geoff Pilling
Jul 13, 2017

Let $N_n$ be the number of ways you can tile an nx2 grid.

Once you know $N_{n-1}$ and $N_{n-2}$ , you can build up to an nx2 grid, by adding either one vertical tiles to an (n-1)x2 grid (2 ways to color this) or two horizontal tiles to a (n-2)x2 grid (4 ways to color this).

This, along with the two trivial cases, translates to the following recurrence relation:

$N_0 = 1$
$N_1 = 2$
$N_n = 2N_{n-1} + 4N_{n-2}$ for $n>1$

$N_{6} = \boxed{832}$

Nice problem. I first counted the number of uncoloured tilings, which is a Fibonacci progression, and then multiplied by $2^{6} = 64$ to account for the two colour choices.

Brian Charlesworth - 3 years, 11 months ago

Ah yes... That certainly simplifies things!

Now you've got me thinking... What might be a more interesting coloring problem where you can't decouple the coloring from the rest of the problem... How about tiling an nx2 grid with differently colored 1x1 and 2x1 tiles... Hmmm....

Geoff Pilling - 3 years, 11 months ago

b l u e {\color{#3D99F6} \mathbf{blue}} b l u e and r e d {\color{#D61F06} \mathbf{red}} r e d Tiles

The answer is 832.

1 solution

0 pending reports

${\color{#3D99F6} \mathbf{blue}}$ and ${\color{#D61F06} \mathbf{red}}$ Tiles