Colorful Electrons
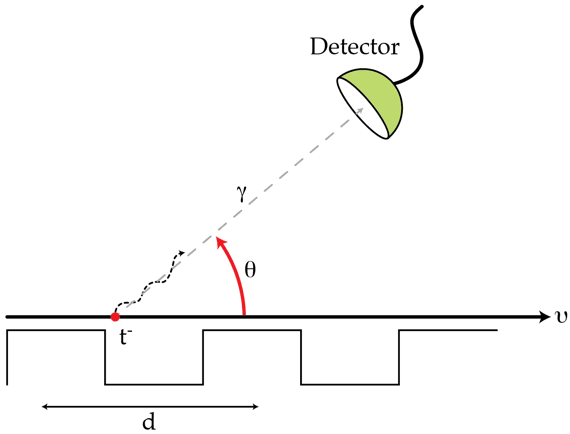
A narrow beam of electrons passes close to the surface of a large metallic mirror with a diffraction grating of period inscribed on it as shown in the figure. The electrons move with ( is the speed of light) at right angles to the lines of the grating. As a result of the etchings, the electrons may emit visible radiation whose wavelength depends on the angle of observation . At which angle in degrees will the observed radiation be green? Assume that the velocity of the electrons is not affected by the mirror.
Details and assumptions
Assume that green light has wavelength )
The answer is 33.27.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
First, we should ask ourselves about the origin of the radiation. Note that the interaction of the electron with the grating can be described by introducing an image charge (of opposite sign). Thus, each electron and its image constitute a dipole which is periodically disturbed by the etchings. In the rest frame of the electron+image, the grating has period given by d ′ = d 1 − c 2 v 2 (Lorentz contraction) . Therefore, the frequency of the "oscillations" of the dipole formed by the electron+image in its rest frame is f 0 = v / d ′ = d 1 − c 2 v 2 v . We can determine the frequency f registered by the detector employing the general formula for the Doppler shift f = f 0 1 − c v cos ( θ ) 1 − c 2 v 2 ⇒ λ = d ( v c − cos ( θ ) ) , where λ = f c . Solving for θ , we find the value θ = 3 3 . 2 7 ∘ . By the way, the emission of visible radiation by electrons passing closely to the surface of a metallic diffraction grating is called the Smith-Purcell effect.