Coloring A Big Board
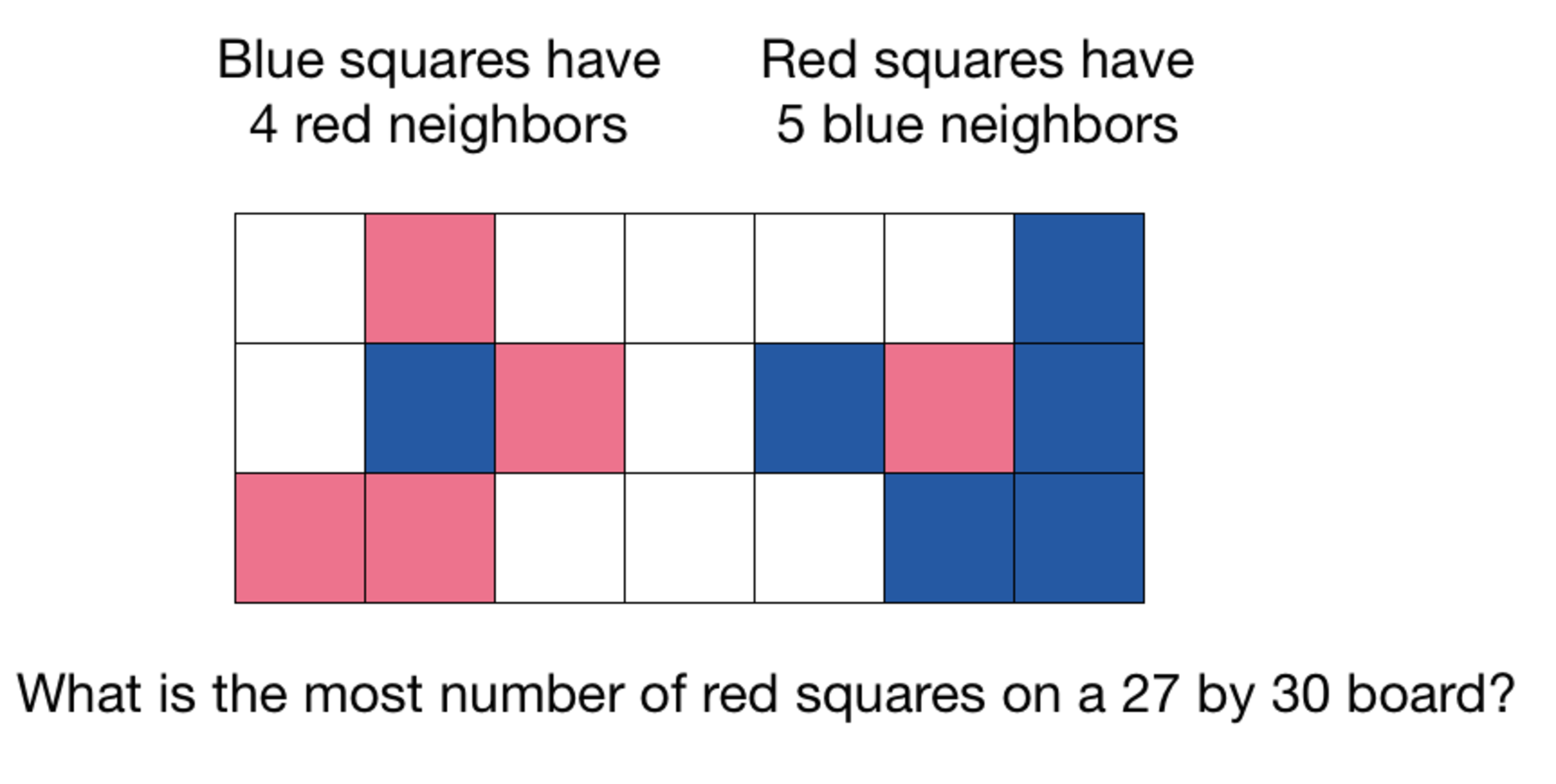
Consider a board in which its squares have been colored red or blue. We know that for each blue square, that is not on the edge, 4 of the 8 squares that are adjacent, are red. Also, we know that for each red square, that is not on the edge, 5 of the 8 squares that are adjacent, are blue. Find the maximum number of red squares on the board.
Details and Assumptions :
2 squares are adjacent if they share at least a vertex. Indeed, each square that's not on the edge has exactly 8 adjacent squares.
The answer is 360.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
We know that in each 3 × 3 square there will be 4 red squares and 5 blue squares, because if in the center is a red square, the edges will always have 5 blue squares, and if in the center is a blue square, the edges will have 4 red squares:
R B R B R R B B B
R B R B B R B R B
As a 2 7 × 3 0 board can be divided in ninety 3 × 3 squares, the number of red squares in the board is 9 0 × 4 = 3 6 0 .
Certainly, a board colored with these conditions can be achieved simply by doing this:
Take, for example, this 3 × 3 arrangement:
R B R B R R B B B
3 0 times to form the 2 7 × 3 0 board.
Join 2 of these matrices side by side successively, and we have colored all the board. An interesting question would be how many different boards are with these conditions?