Coloring a flag
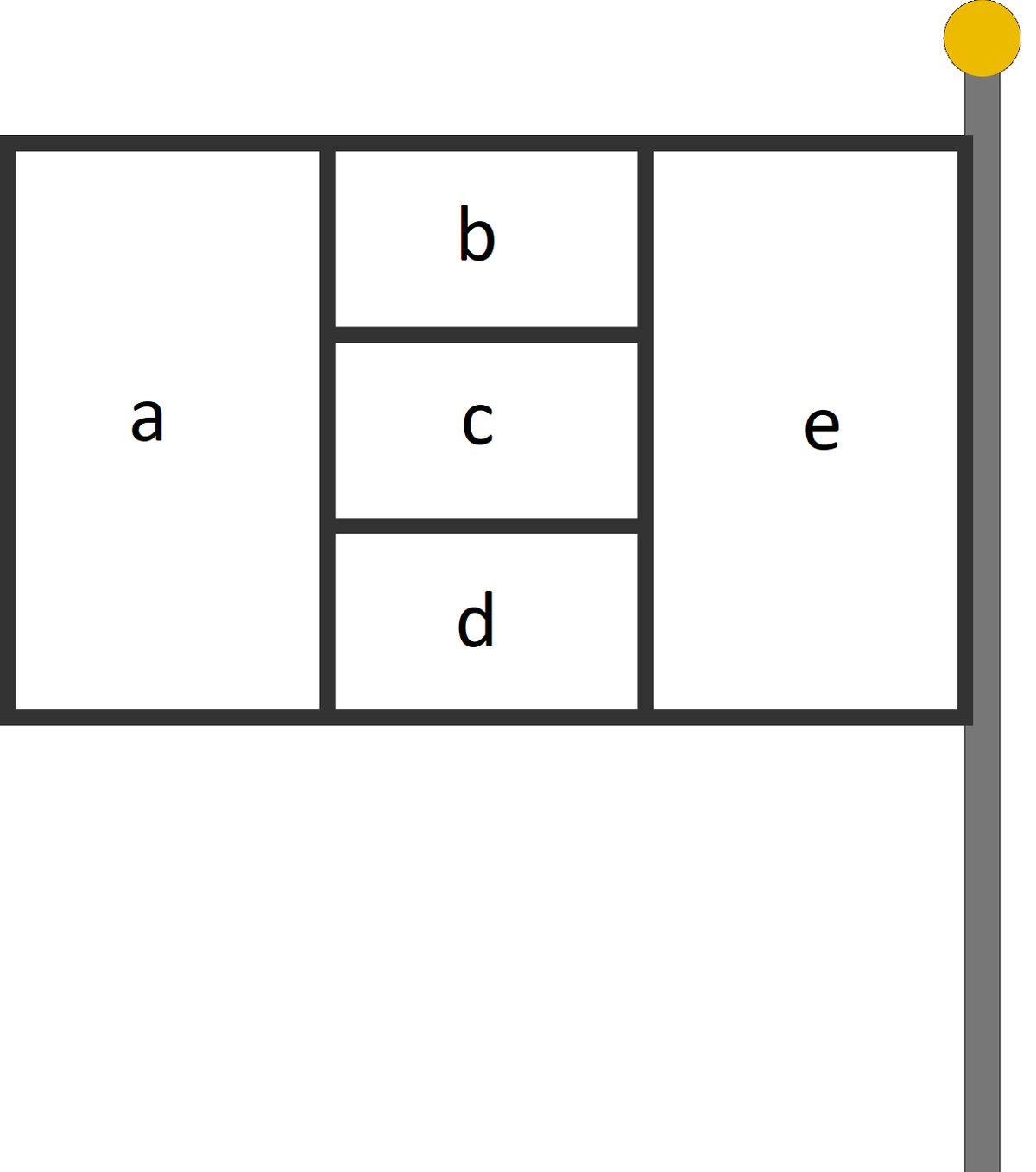
You have a set of 10 paints of distinct colors and a flag with 5 regions, shown to the right.
In how many ways can you color all 5 of the regions such that regions that share an edge are different colors?
Note
: The flag is attached to a flagpole, which prevents the flag from being rotated or flipped.
The answer is 41040.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
9 solutions
I separate to 2 cases only:
Case 1 : Middle's uppermost and lowermost section have same color: P 2 1 0 × 8 2 .
Case 2 : All of the middle's sections have different colors: P 3 1 0 × 7 2 .
Interesting use of the rule of product ! I solved it the same way.
in case2 why do we have to multiply by 2... i am a beginner so I did not understand.
Log in to reply
Because there are exactly 4 colors. If left and right are the same, the middle are all different. That's 10 x 9 x 8 x 7. If top center and bottom center are the same, then left and right are different from each other (and different from the center block). That's 10 x 9 x 8 x 7 more. There is no overlap in those so you need to count them both.
I think the solution forgets to calculate the differents way the colour can be arranged in the flag. Lets just forget about the flag for a second. Out of 10 colours there are 720 ways to pick 3 different colours, as 10 9 8=720. Same calculation we get 5040 ways to pick 4 colours, and 30240 ways to pick 5. Now for the flag to have different colour that dont share the same edge, we need at least 3 different colours. Lets say for example these colours are red, blue and yellow, there are different ways to put these colours into the flag: red on top and bottom, blue on the sides and yellow in the middle, or still red on top and bottom, but blue in the middle and yellow to the sides, and so on we got the equation 3 2 1= 6 different ways to put 3 same colour in the flag. As we saw earlier there are 720 different combination of 3 colours out of 10 colours, so the total ways to put 3 different colours into the flag are 720*6=4320 ways. Same calculation we get 120960 ways for 4 colours and 3628800 god damn ways for 5 colours. So the total possibilities are 4320+120960+3628800=3 754 080 ways, not just 41040 Can somebody tell me if im correct or where did i get it wrong?
Log in to reply
Hi Nhat, when there are 3 different possible colours out of 10 to paint the flag with, than the 3 * 2 * 1 doesn't come to play. You can either go for: 10! divided by (10 -3)! or you can just count back using 10 * 9 * 8, both of which give you the TOTAL amount of 720 possibilities. No need to multiply that with anything anymore, because even when using a colour 2 times in this problem it will only allow you 3 different placing possibilities. E.g. putting yellow in the leftmost section automatically forces you to put yellow in the rightmost section, which accounts for the same flagpattern as putting yellow in the rightmost section (forcing you to also use yellow for the leftmost section) This means both options are similar and one of them should not be taken into consideration during our calculating. Since than, in truth, there are really only 3 different positions in which to put a certain colour we could just go with the 10 * 9 * 8 and be done with it because the other options are indistinguishable.
Obviously using 4 colours does not force you to choose from just 3 placing options; it gives you 4 options with 2 different ways to place the double colour.
And using 5 colours does not leave you the option of doubling colours.
I hope this helps, and don't worry I got it wrong too :) I miscalculated the amount of options using 4 colours and had to read into it before seeing my mistake.
Log in to reply
Thank you for your reply, i been off since then and only see the notification now :). Anyway i just re-read the problem as well as my answer and i can see where i did the mistake. Back then i was new to the possibility-calculation so i didnt fully understand what 10 * 9 * 8 means. You are right, the options are indistinguishable therefore only the calculation for all possibilities is already enough. It was very confusing to me with all the big numbers, so a tip for my pass-self as well as anyone who might struggle like i did: simplify the problem with smaller numbers, for example you have 4 colours to paint 2 square, you can either use the math 4 * 3 or you can list out all the possibilities one-by-one yourself. Solving easier problems with help you understand/solve the bigger problems.
The first big portion can be painted in 10 ways now coming to middle....from top....first part can be painted in 9 ways.... second in 8 ways....the third again in 8 ways.....now the last big rectangle in 7 ways... In this way 10 9 8 8 7=40320 Please suggest how this approach is wrong.
Log in to reply
Because the left and the right part can also be same colour (as they dont share the same edges) so we only need 3 different colors to fill the flag, we can also fill it with 4 colors or even 5 (each part has a different colors).
it can be paint only once after that what about the 41039 ways lolzx
I made two mistakes in calculating. My first mistake was to calculate number of combinations instead of number of permutations. My second mistake was to think that it was not possible to color it with exactly three colors.
Consider the underlying graph of the flag, the left graph in the following picture, which we will call F (for "flag"):
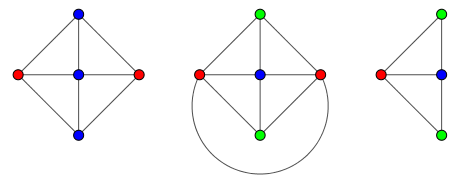
We will compute the chromatic polynomial of this graph by using deletion-contradiction formula. (Remember that the chromatic polynomial P ( G , k ) of a graph G , evaluated at k , gives the number of proper colorings of G with k colors. So we just need to evaluate P ( F , 1 0 ) to get the answer.) For any two adjacent vertices u , v in a graph G , the chromatic polynomial P ( G , k ) is equal to P ( G − u v , k ) − P ( G / u v , k ) , where G − u v is the graph G with u v removed, and G / u v is the graph G with u , v glued. (The proof is obvious: P ( G − u v , k ) counts colorings where u , v may have any color, and P ( G / u v , k ) counts colorings where u , v have the same color; this leaves P ( G , k ) , where u , v have different colors.) We can restate this as P ( G , k ) = P ( G + u v , k ) + P ( G / u v , k ) where u , v are not adjacent.
Also, the chromatic polynomial of a complete graph K n is easy: P ( K n , k ) = ( k − n ) ! k ! , since we have k choices for the first vertex, k − 1 choices for the second vertex, and so on. (If k < n , the polynomial evaluates to zero.) Moreover, K n − e , the complete graph missing one edge, is also easy: P ( K n − e , k ) = ( k − n + 1 ) ! k ! ⋅ ( k − n + 2 ) , which can be done combinatorially (pick one endpoint of the missing edge, color it and its neighbors, then color the other endpoint), or by simply using the deletion-contradiction formula above.
Finally, let F 1 , F 2 be the middle graph and the right graph in the above picture. Note that if we pick the red vertices as u , v , then F + u v = F 1 and F / u v = F 2 . So P ( F , k ) = P ( F 1 , k ) + P ( F 2 , k ) . But the latter two are both complete graphs with one edge missing (the green vertices form the missing edge): P ( F 1 , k ) = k ( k − 1 ) ( k − 2 ) ( k − 3 ) 2 and P ( F 2 , k ) = k ( k − 1 ) ( k − 2 ) 2 . Thus P ( F , k ) = k ( k − 1 ) ( k − 2 ) ( k 2 − 5 k + 7 ) . Plugging in k = 1 0 gives 1 0 ⋅ 9 ⋅ 8 ⋅ 5 7 = 4 1 0 4 0 .
We must choose three different colors for the left, top, and center regions. There are 1 0 × 9 × 8 ways to do this.
For the remaining regions, we have four options.
-
Choose the same color for left and right, and the same color for top and bottom. No additional choices are necessary. ( 1 )
-
Choose the same color for left and right, and a new color for the bottom. This gives 7 additional choices.
-
Choose the same color for top and bottom, and a new color for the right. This gives 7 additional choices.
-
Choose two new colors for right and bottom. This gives 7 × 6 additional choices.
Adding these together, we have 1 0 × 9 × 8 × ( 1 + 7 × ( 2 + 6 ) ) = 7 2 0 × 5 7 = 4 1 0 4 0 possible colorings.
I like your approach!!!
Can we make it even simpler?
When you come to the bottom middle there are two options: (1) it is different from the top : 7 choices, leaving 7 for the right (2) it is the same : one choice, leaving 8 for the right
So: 10 * 9 * 8 * 7 * 7 + 10 * 9 * 8 * 1 * 8
... sorry about the formatting
Log in to reply
Certainly. The only reason why I did not take this approach is that it would break the symmetry in this problem (my 2nd and 3rd case).
resolved by brute force in Python :
(I don't know why the indentation doesn't work, so I've put an image)
P=0 for a in range(10): for b in range(10): for c in range(10): for d in range(10): for e in range(10): if a!=b and a!=c and a!=d and b!=c and c!=d and e!=b and e!=c and e!=d:P+=1 print(P)
>> 41040 >>
Case 1 gives you 10x9x8x7x7 different designs. Case 2 gives you 10x9x8x8 different designs.
Case 1+Case 2 = 41040 ways
can you shed more light on case 2 ,please!
Considering two different cases:
Case 1: Leftmost and rightmost have same colors 10(left-large) *9(middle-center) *8(middle-top) *8(middle-bottom)=5760
Case 2: Leftmost and rightmost have different colors 10(left-large) *9(right-large) *8(middle-center) *7(middle-top) *7(middle-bottom)=35280
Total=5760+35280=41040
Consider the center section, we can have either A) 3 different colors, or B) top and bottom the same color. In Case A, there are 7 possible colors remaining for the two outer sections, in case B, there are 8 possible colors remaining.
Hence A = 10 x 9 x 8 x (7 x 7) = 35280 and B = 10 x 9 x 1 x (8 x 8) = 5760
Total = 41040
Three distinct colours in the middle (10x9x8): => 10x9x8x7x7=35280 (because right side can have same colour then left side). Two distinct colours in the middle (10x9): => 10x9x8x8=5760 (right side again can have same colour than left side). Add both together: => 35280+5760=41040.
This is ultimately a counting problem so the solution comes naturally by breaking down into cases. In my case I will only consider two cases. Case 1: First choose a color to paint both the leftmost side and rightmost side, then pick a color to paint the center rectangle, and then pick two colors for the two remaining rectangles. For our first choice we have 10 options. For our second choice we cant pick whatever we picked in the first choice, so we have 9 options. And for the third and fourth choice we cannot pick the two colors we chose previously, so there are 8 options and then 8 options. Total = 1 0 ∗ 9 ∗ 8 ∗ 8 =5760.
Case 2: First choose a color to paint the leftmost side. Then choose a different color to paint the rightmost side, then pick a color to paint the center rectangle, then pick two colors for the two remaining rectangles. For the first choice we have 10 options. For the second choice we are forcing ourselves to pick a different color, so 9 choices. For the third choice we may pick from the 8 remaining colors. And for the last two choices we may pick twice from the 7 remaining colors. Total = 1 0 ∗ 9 ∗ 8 ∗ 7 ∗ 7 = 3 5 2 8 0 .
Adding up both of these totals we get the grand total 4 1 0 4 0 .
Separating the coloring into three cases.
case 1: Using exactly 5 different colors . 10x9x8x7x6=30240
case 2: Using exactly 4 different colors . We have two possibilities leftmost section and rightmost section have the same color or the middle's section uppermost and lowermost sections have the same color. 10x9x8x7x2=10080.
case 3: Using exactly 3 colors . Leftmost and rightmost have the same color and middle's section uppermost section and lowermost section have the same color. 10x9x8=720
30240+10080+720=41040