Coloring a Hypercube

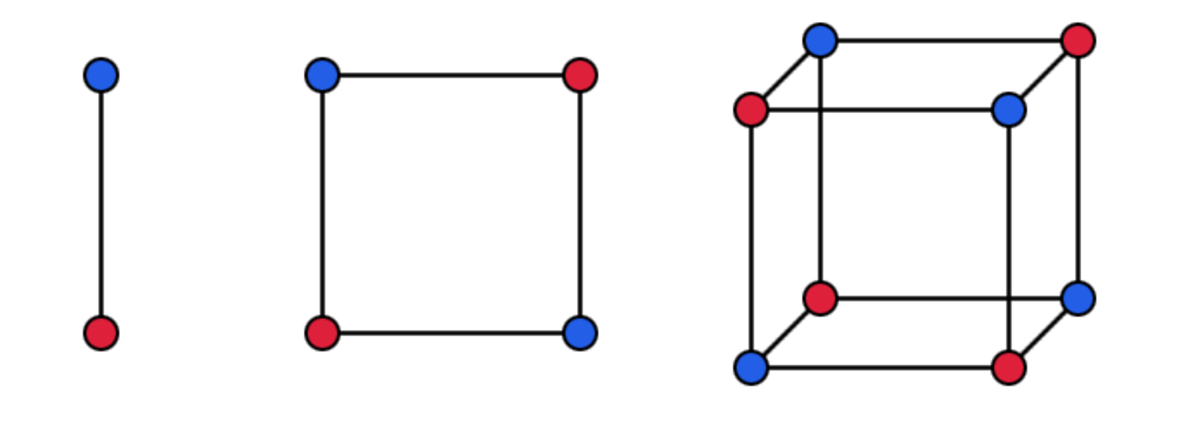Every hypercube of dimension greater than or equal to one can be colored with $2$ colors. An informal proof of induction is as follows. A one dimensional hypercube (a line segment) can be colored with $2$ colors, but not $1$ . Every hypercube of dimension $n+1$ can be made by 'stitching together' the corresponding vertices of a hypercube of dimension $n$ . If you invert the vertice colors of one of the two $n$ -dimensional hypercubes you're joining together then your final hypercube of dimension $n+1$ is also colored appropriately. This process is perhaps best explained in the picture.