Coloring A Map
Each region below must be fully colored in such that no two adjacent regions share the same color. What is the smallest number of colors necessary to perform the coloring?
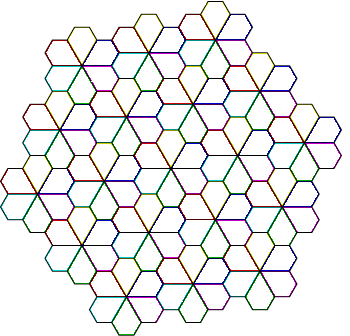
Clarification : The outside does not need to be colored.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
Hahah! Nice antisolution.
real smart (y) ; but you have only one try (now at least) [perhaps it was edited after this solution :D]
suppose he made even bigger pattern upto inf then
In order to have some terms in which to think the problem and also some understanding of the formulation of the way of the "map" coloring it should firstly be made explicit some organization of this way to color the map. For that observe that all the "regions" can be organized in 19 hexagons made from 6 regions each in such a way that in the center of the figure there will be a hexagon , around it 6 other and also 12 other outer hexagons and take this hexagons as the structure to which the coloring of the figure can be taught of. Then for some proper coloring of the entire figure there should be firstly a proper coloring of any hexagon and this in such a way that for any 2 hexagons which are next to each other their corresponding next to each other regions should not have the same color making it necessarily to respect these 2 conditions or in other words that in order to achieve a proper "construction" this can be taught of as trying to color the hexagon and understanding for which coloring of the hexagons the coloring of the entire map is proper. Now , the smallest number of colors used can't be 1 and can't be 2 also since for taking 2 as the smallest number then any hexagon including the ones that are not the outer hexagons will have to be colored with 2 colors where for any region of an inner hexagon there will be a configuration made from this region (where this region is central) which will use one of the 2 colors and 5 other regions that surrounds it where any of this 5 regions will have to use the same and only different color from the central region but which some will nonetheless touch some of the other 4 regions therefore making it impossible. Since the number of colors isn't 1 or 2 , it can be tried to construct a proper coloring using 3 colors. However note that there is no possible coloring of a hexagon with 3 colors since it will not respect condition 2 because for any such proper coloring of an inner hexagon there will always be at least 1 region with some color and 2 that touch that region with 2 different colors , therefore there will always be 3 consecutive colors somewhere in the hexagon which implies that again there will be for such a region a configuration made from that region as central in the configuration and 5 other surrounding regions where the 2 regions which belong to the same hexagon have different colors therefore being that from the other 3 regions that are in the exterior of the hexagon the 2 that touch the central and one of the other regions which belong to the hexagon of the central region will have 2 different colors and the other region which touches the central and the 2 other regions that are in the exterior of the hexagon to which the central region belongs will have next to it regions with all the available 3 colors therefore making it impossible. This means that in order to have a proper coloring of the entire map there will be needed to color each inner hexagon with 2 colors and to use a maximum of 3 colors. What remains to be done is to see if such a case is indeed one that leads to a proper coloring construction. If for any hexagon there will be used 2 colors consider such a coloring for one of the inner hexagons and the way it behaves with the hexagons that are next to it and observe that , in order to avoid the problem which was found when trying to color the region just using 2 colors , taking again the configuration made by one region of an inner hexagon and all it's surrounding regions (from which 2 belong to the same hexagon and 3 to other hexagons , just to remind) the 2 of them that touch 2 regions of the hexagon with the central region will have to have a third color therefore making that the hexagons that includes them have at least a different color. Since one of the hexagons will also have the other region from the 3 regions outer to the hexagon to which the central region of the configuration taken into consideration that hexagon will have 2 colors therefore conditioning since it also touches the hexagon which has just one region outer to the hexagon that has the central region in the configuration the color of the other hexagon. Therefore for any configuration of 3 hexagons that are next to each other there is a proper coloring where each hexagon uses 2 colors out of 3 and where each of them has just 1 color in common with the other 2 and for taking for example the central hexagon it can be proved that from this that there is also a proper coloring for all the hexagons next to it generating for some way of numbering all the hexagons next to the central one the same coloring of all the odd ones and the same for all the even ones , and from this also generating a coloring for the other so called outer hexagons which uses also the specific coloring of the central hexagon.
By the way , I somewhere said in this proof that there is necessary that if there are used 3 colors for a hexagon then there will always be a configuration of 3 colors that come one after the other without proving it and I also it can be said that for the fact that there should be not just 1 color in a proper coloring and while the 1 is easier to see it seems the other one is harder so I'll say here that it can be proved by checking the cases or in a nicer way by looking at the way for placing the 3 colors in the places since for taking any 2 colors if their distance is 1 , that is if they have a space between them there will need to be by definition another color between them and if there is no such configuration and the colors that have one space between them are the same , that is it is the same color then the places that are between these positions must also by definition have the other colors making it necessary to have 2 colors that have a distance of 1 place between them. Anyways , observe also that this is a little more constructive way of solving the problem. I think it can be done also by understanding it structurally but also on the bases of taking a hexagon and also of the configuration , and that would be nicer and simpler i think.
Since there is a place on the map, where 3 regions are all adjacent with each other, we need at least 3 colors. And from example below you can see that 3 colors is enough to color this image.
 Example of coloring
Example of coloring
I don't know any legit solution, so I just made a good guess. By the four colour theorem, which I don't know how to prove, the answer is at most 4. And as another user said, it is obviously not 1. Then you try to colour it with two. You can find places (between individual . . . flowers?) such that three regions all touch each other. Thus, if we have only two colours, then it wouldn't work. Now, we are left with 3 or 4.
The picture "repeats," so I don't think it would really matter if we removed a lot of the flowers and made the picture smaller. I focused on a group of three or four flowers that touched each other and coloured those in with three colours in my head. Lo and behold, it worked, so I guessed it was three. LOL
The figure given above is one pattern(kind of like a flower with six petals) stacked together many times. Consider one of these flowers. You can use three colors to cover up this flower without two adjacent petals sharing the same color. If you look closely enough, you can see that using those exact same three colors you can cover up all the flowers without any two adjacent petals of two adjacent flowers sharing the same color. Hence the correct answer is 3.
In mathematics, the four color theorem, or the four color map theorem, states that, given any separation of a plane into contiguous regions, producing a figure called a map, no more than four colors are required to color the regions of the map so that no two adjacent regions have the same color.
Thus, the answer has to be smaller or equals to 4. Clearly, the answer cannot be 1. So, we are left with 2, 3, 4. Since we have 3 tries, we can try each answer and we realise that 3 is correct.