Coloring a polyhedron
This 3D solid is colored on each of its 18 faces.
What is the minimum number of colors needed so that no two edge-sharing faces are the same color?
Note : Faces that share a vertex but not an edge can be colored the same.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
Besides finding an actual solution, is there another way to prove that 2 is the minimum number of colours required?
Log in to reply
I think the solution that you want is just below it
You can simplify this problem by using a strip of paper rather than a figure, with the end connecting to the beginning. If there are an odd number of sections on the paper and you want to alternate between two colors, this is simply impossible. However, doing this with an even number of sections is possible. The same principle can be applied here. Since the top and bottom view of the figure have an even number of symmetry lines, using only two colors is possible.
The original version of the problem was much much better. I wish the people at Brilliant would not always change things, at least not this much.
Log in to reply
What was the original problem? I haven't seen it.
HOLLY COWS I was thinking the exact same thing! Even the colors were the same!
We see that in this figure
-
No three faces can be found such that all of them atleast shares an edge with each of the other two.
-
There exist two faces which share an edge.
So the minimum number of colors is
2
That logic doesn't work. More colors may be needed in some cases even if both of the conditions are fullfilled. For instance, if there is an odd amount of edges beginning from the same vertice, you'll need more than 2 colors to satisfy the problem.
Log in to reply
I think you misunderstood. I mean to say that even if a face 'A' is adjascent to more than 1 face, then none of the faces which are adjascent to face 'A' are adjascent to each other.
Log in to reply
As Joel said, this isn't sufficient. You are saying that any triangle-free graph is 2-colorable. But the proper statement is that a graph needs to be without odd cycles to be 2-colorable.
Consider the 10-sided solid formed by gluing together 2 five-sided pyramids to a shared base. Each face of this figure is adjacent to exactly two other faces: the two next to it on its pyramid, and its counterpart in other pyramid. But since it has an odd cycle, it cannot be 2-colored.
it is extrodinary superb
English is very ambiguous, if you read the problem statement as no "two edge" sharing faces, then the answer is 1 color
This figure is unique because that every point connecting 2 or 4 faces, even number, then 1212, two colors is enough. eg.Octahedra But the cube is different, one point with 3 faces, so it needs 3 colors. These are the simple examples, for the complex ones with many faces, (1)all even number, (2)some are even number, some are odd number, it needs lots time to think.....
Since all vertices have an even number of faces surrounding them, and since moving from one face to a neighboring face is the same as moving around a vertex, then only two colors are needed to not encounter the paradox where a face must not be its own color, as would be encountered if any of the vertices had an odd number of faces surrounding them.



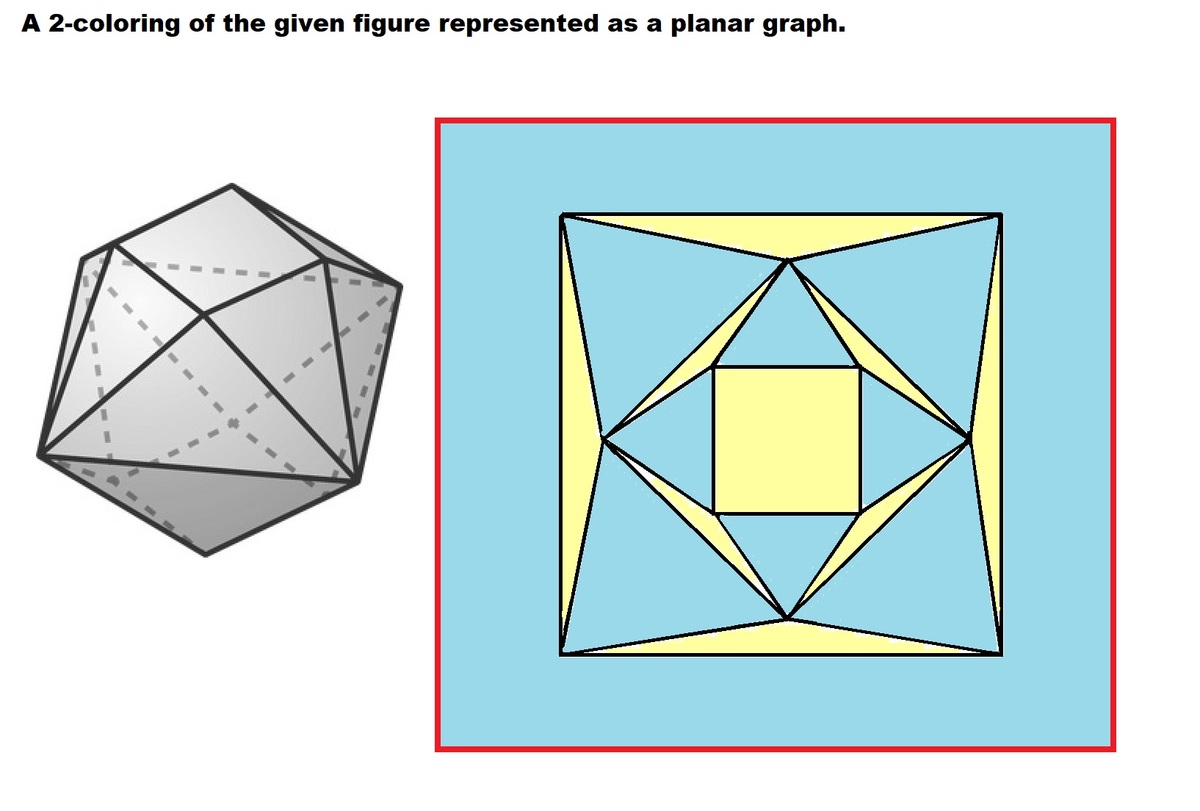
Clearly, not all faces can be the same color, so there must be at least two colors. Here is a two color solution: