Coloring Chessboard With Black And White Square Removed
Probability
Level
1
Suppose that one black square and one white square of an 8-by-8 chessboard are removed. Is it possible to tile what remains of the board with 1-by-2 dominoes?
Yes; sometimes
Yes; always
No; never
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Most of us know that removing two of the same coloured squares will result in a chessboard that is not solvable. Does this mean we can assume that all grids with the same number of each colour are always solvable?
Certainly not. Obviously if we have one isolated black square and one isolated white square then it's not solvable, but, even with the restriction with all squares needing to be connected, we consider the following cas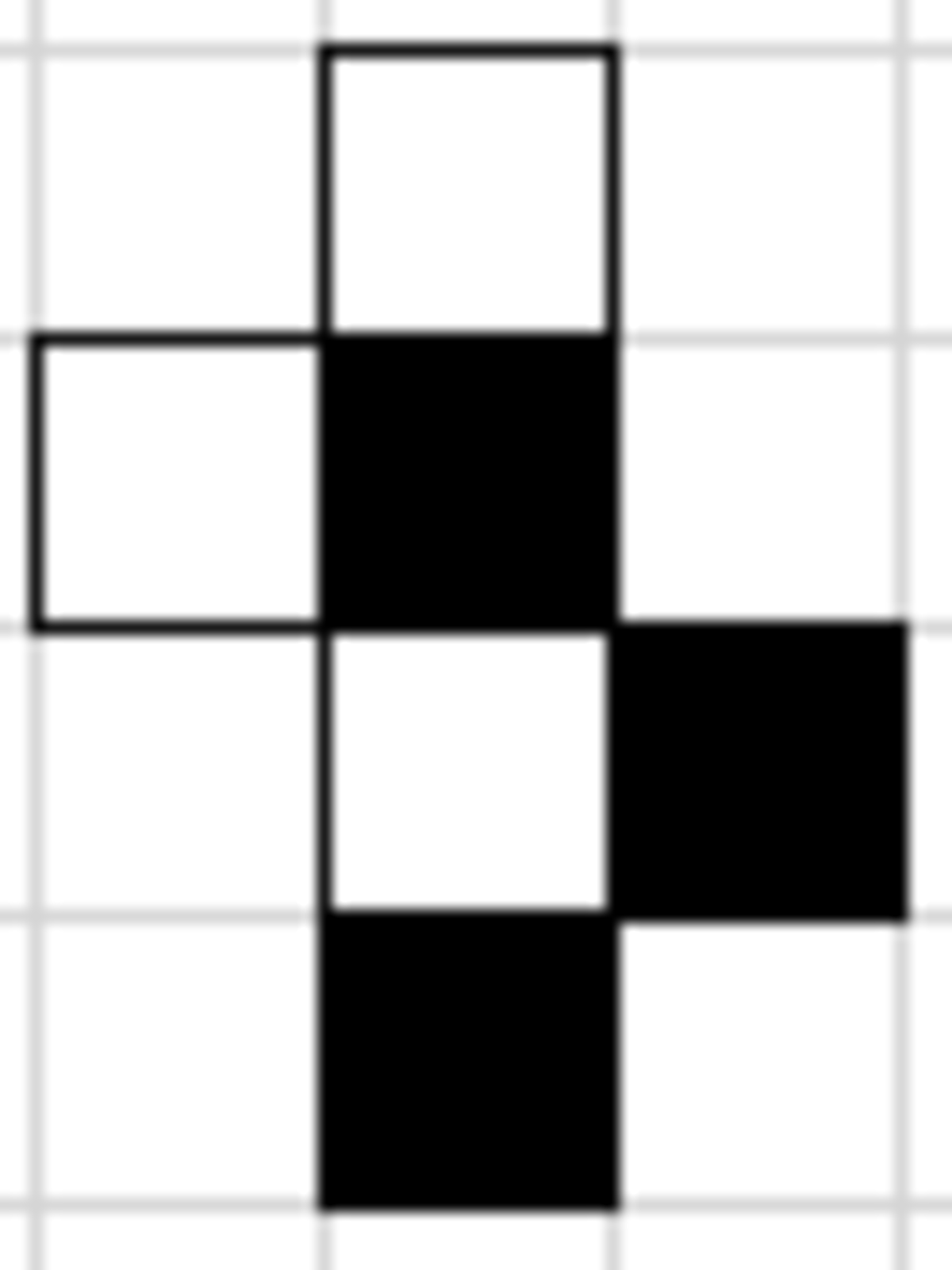e:
Two of the black squares would both require to have a domino cross the same adjacent square, as there are no other adjacent squares, which is much the same with two of the white squares, so even though it's connected and there are as many black squares as white squares, it is
still
not solvable
In this example, however, this situation will not occur.
Here is an example grid: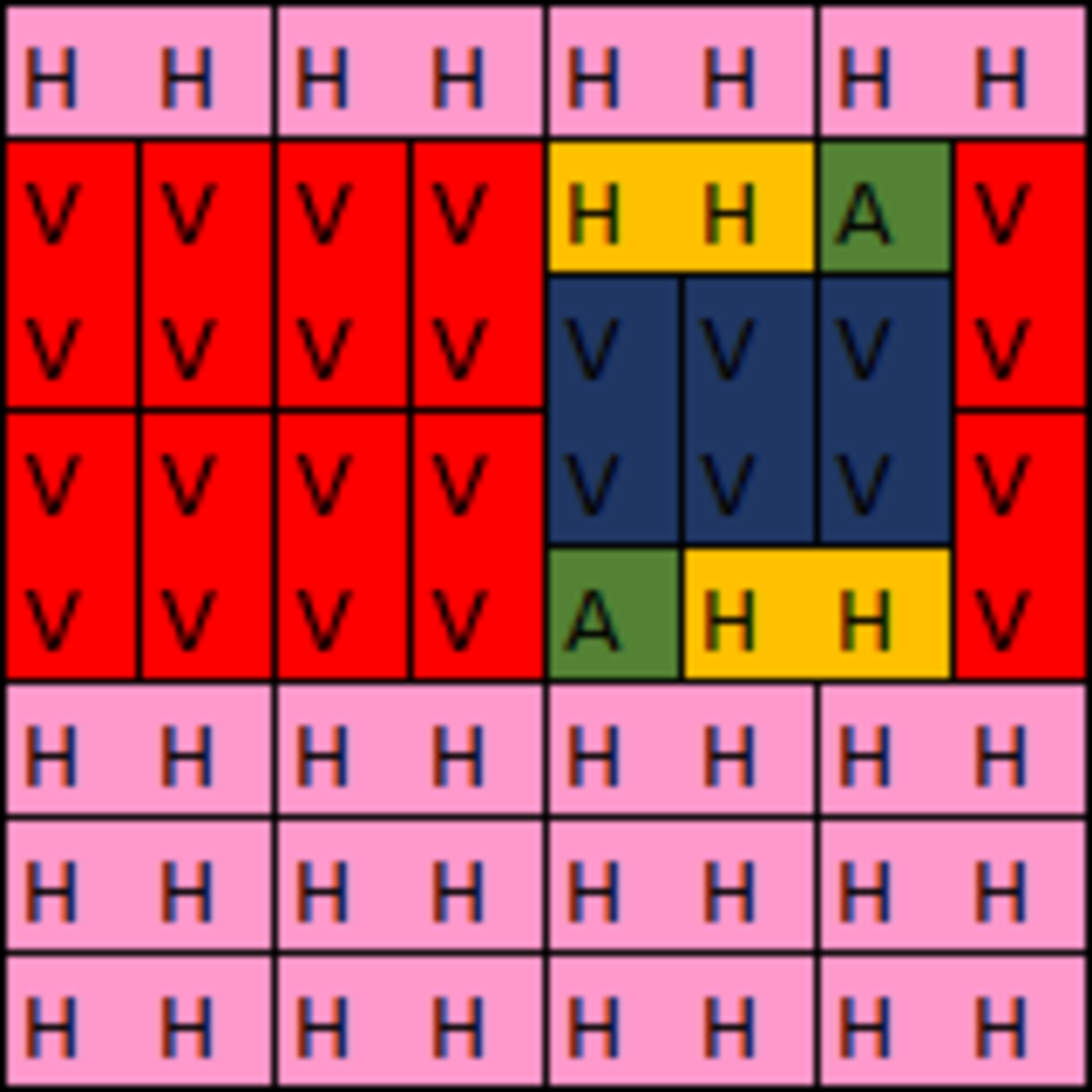
the removed blocks will always be two corners of a block that has one even dimension and one odd dimension. It is always possible to fill in a block like this, as you can fill the rest of the outer edges of odd length by dominoes (yellow), which reduces the even dimension by two, and then you can fill the remaining space with dominoes such that the dominoes are oriented longways in the even dimension (navy). (I leave it up to the reader to consider how this works when the dimensions are small). Now we just need to show that the outer shell is always able to be filled.
Because one of the dimensions of the block will be even, we can extend the block to the edges in this dimension with dominoes oriented longways in the even dimension (red). Now we are left with two regions with one length equal to 8. (either region could be empty). These regions are also easy to fill, because we can just place dominoes that are longways on the 8 length, from end to end (pink).