Coloring the Great Rhombicosidodecahedron
Probability
Level
3
This is the Great Rhombicosidodecahedron:
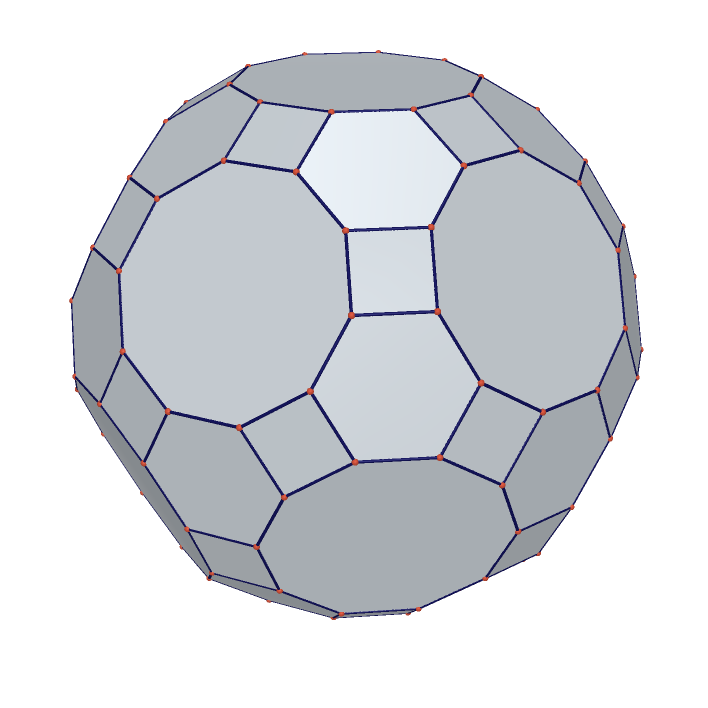
What is the minimum number of colors you need to color all sides of a Great Rhombicosidodecahedron such that no two sides that join on an edge have the same color?
Image credit: http://m100.nthu.edu.tw/
2
3
4
5
6
7
8
None of these answers
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
You need at least three colors since three faces meet at a vertex, and all three of those would need to be a different color.
However, the cool thing here is that you can do it with only 3 colors, by coloring the squares one color, the hexagons another color, and the decagons a third color, like this:
Image credit: commons.wikimedia.org