Disconcerting disc
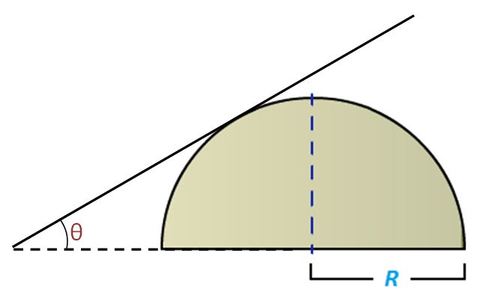 Find the Moment of Inertia (in S.I. unit) of a uniform semicircular disc of mass
and radius
about an axis parallel to its plane and touching it at circumference while making an angle
with its diameter as shown in the figure.
Find the Moment of Inertia (in S.I. unit) of a uniform semicircular disc of mass
and radius
about an axis parallel to its plane and touching it at circumference while making an angle
with its diameter as shown in the figure.
The answer is 175.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let C be the center of mass of disc. So d = 3 π 4 R .
Now, by parallel axis theorem, I O = I C + M ( d c o s θ ) 2 ⟹ I C = I O − M d 2 c o s 2 θ ∴ I C = M ( 4 R 2 − d 2 c o s 2 θ ) .
Again by parallel axis theorem, I P = I C + M ( R − d c o s θ ) 2 = 4 M R 2 − M d 2 c o s 2 θ + M ( R 2 + d 2 c o s 2 θ − 2 R d c o s θ ) ∴ I P = 4 5 M R 2 − 2 M R d c o s θ
Putting the given values in the above expression we would get I P = 1 7 5 k g m 2