Colossal O, Miniscule
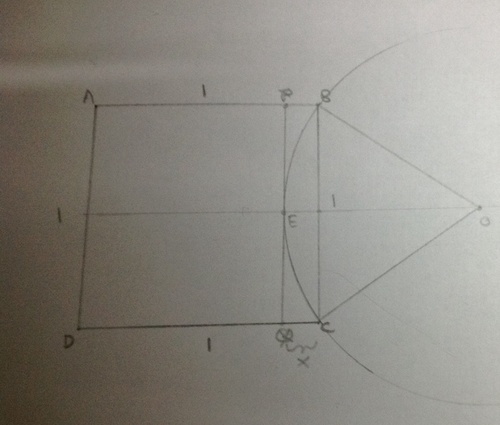In the above diagram,
is a unit square. A circle
with radius
has side
as a chord. The distance which the circle intrudes into the square is given as
, as in the diagram. What is the
infimum
of
?
The answer is 0.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Obviously, as r increases, x decreases, because the chord is of the same length, but the circle is bigger. Thus, the minimum value of x would be obtained if the size of the circle O is huge, thus making the curve inside the square a straight line. Thus, the chord BC would coincide with the circle, and x = 0
However, it must be noted that x cannot be exactly 0 .
If you take the midpoint of AD and extend a line parallel to AB and CD from it to the midpoint of the circle, a right triangle would be formed with legs 2 1 and r − x , and hypotenuse r . Thus, r 2 = 4 1 + ( r − x ) 2
Simplifying, we get 4 ( x ) 2 + 1 = 8 r x
Thus, if x tends to zero, 8 r x should be equal to 1. Thus, x would be incredibly miniscule. Thus, 0 < x < < 1