COM of a a Wire
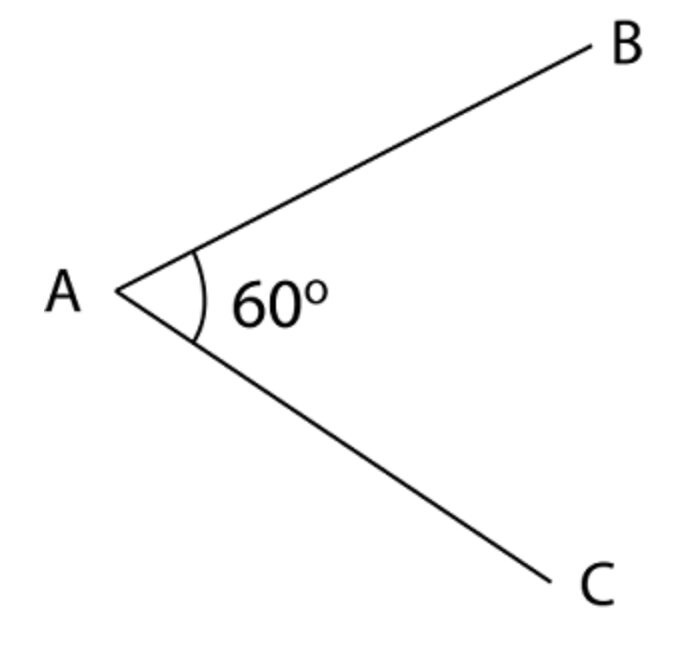
A uniform wire of length
is bent into shape
V
as shown in the figure.
The distance of its
from the vertex
A
is
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let's assume a co-ordinate system where A is the origin and the angular bisector of A B and A C is the x-axis.
The length of A B is 2 l and the location of its center of mass is the midpoint ( 4 l cos 3 0 ∘ , 4 l sin 3 0 ∘ ) .
Similarly, the center of mass of A C is ( 4 l cos 3 0 ∘ , − 4 l sin 3 0 ∘ ) .
The centre of mass of the whole wire is the midpoint of the above two centers of mass (as the wire is of uniform mass distribution).
∴ C ≡ ( 4 l cos 3 0 ∘ , 0 )
⟹ required distance = 4 l cos 3 0 ∘ = 8 l 3