Try This Combinatorics Problem
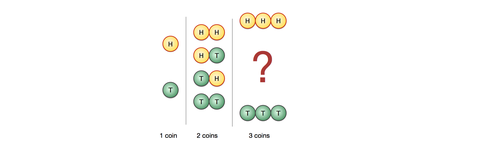 When we flip 1 coin, there are 2 possible outcomes.
When we flip 1 coin, there are 2 possible outcomes.
When we flip 2 coins, there are 4 possible outcomes.
When we flip 3 coins, how many possible outcomes are there?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Discussions for this problem are now closed
I like that! I love all your challenges only some get into my head. Well, thats fun too.
the solution of " Alternatively " is the best
Since there are HHH and TTT remaining possiblities is 6. total 8. 2 are given so remaining 6
We can think of this recursively to derive a generalization of the problem:
If we flip one coin, there are two outcomes: Heads or Tails.
If we flip two coins, we can think of this as flipping the first coin (so two outcomes) and then flipping another coin where there are another two outcomes. Laws of probability tell us that we should multiply two by two to get four outcomes if we flip two coins.
Flipping three coins is the same as flipping two coins and then flipping another coin, so we get 2 × 4 = 8 outcomes.
To generalize, let a n be the number of possible outcomes with n coin flips. Then this follows the recursive sequence a n = 2 a n − 1 , with a 1 = 2 . Using this, we find the explicitly defined sequence a n = 2 n .
There are 8 possibilities when 3 coins are flipped I.e., HHH, HHT, HTT, TTH, THH, HTH, THT, TTT
(H + T)^ 3 = H H H + 3 H H T + 3 H T T + T T T for 8 outcomes;
(0.5 H + 0.5 T)^ 3 = (H^3 + 3 H^2 T + 3 H T^2 + T^3)/ 8 for a sum of 1 where 0.5 could become 0.49 or 0.51.
There are 8 possible outcomes.
We can list the outcomes out as HHH, HHT, HTH, HTT, THH, THT, TTH, TTT.
Alternatively, we can use the rule of product. Since there are 2 possibilities for each coin, there are a total of 2 × 2 × 2 = 8 possible outcomes.